Lesson 3.2: Confidence Intervals
Supplementary Notes 3.2
Confidence Intervals
Let’s begin our discussion of confidence intervals with an excerpt from a newspaper article (Hume, 2006) published by The Globe and Mail.
A Whale of Support for Aquarium Expansion
Poll shows backing is strong for creation of bigger, deeper pools for sea life
By Mark Hume (2006). Adapted from The Globe and Mail.
The Synovate poll, based on interviews with 600 Greater Vancouver Regional District residences (including 300 in the city), shows that 85 per cent of respondents moderately or strongly support a proposal to expand Canada’s largest aquarium….
In this random sample of 600 Greater Vancouver Regional District (GVRD) residents, 85% support the aquarium expansion. We know that this ![]() is just a particular sample estimate of the population percentage
is just a particular sample estimate of the population percentage ![]() of GVRD residents who support the aquarium expansion, and we know this estimate would vary somewhat from sample to sample according to the sampling distribution of
of GVRD residents who support the aquarium expansion, and we know this estimate would vary somewhat from sample to sample according to the sampling distribution of ![]() .
.
Acknowledging this variability in ![]() , it seems unwise to put all our money on the exact value of 85%. Rather, we should estimate the population percentage
, it seems unwise to put all our money on the exact value of 85%. Rather, we should estimate the population percentage ![]() with an interval of possible percentages that is likely to capture
with an interval of possible percentages that is likely to capture ![]() . We can use the 68–95–99.7 rule (empirical rule) from Lesson 2.3 plus our newly acquired knowledge of the sampling distribution of
. We can use the 68–95–99.7 rule (empirical rule) from Lesson 2.3 plus our newly acquired knowledge of the sampling distribution of ![]() from Lesson 3.1 to construct such an interval.
from Lesson 3.1 to construct such an interval.
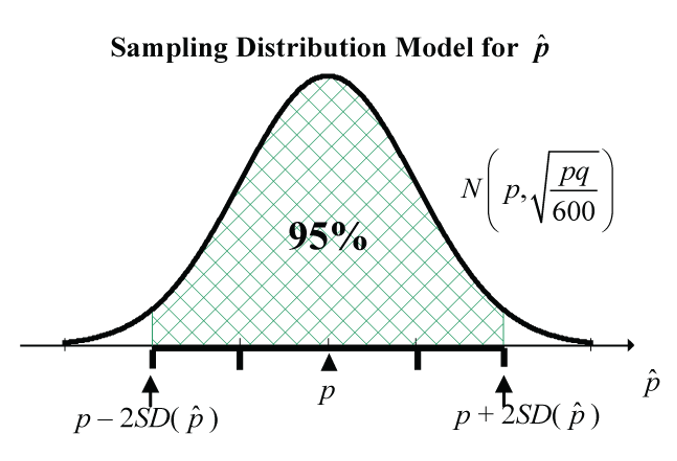
The sampling distribution says that about 95% of the potential values of ![]() will be within two standard deviations of
will be within two standard deviations of ![]() . Recall that the standard deviation of
. Recall that the standard deviation of ![]() is the standard error of
is the standard error of ![]() ,
, ![]() , where
, where ![]() .
.
We approximate the unknown ![]() by its sample estimate
by its sample estimate ![]() . So, “two standard deviations” is
. So, “two standard deviations” is ![]() .
.
So, 95% of the potential values of ![]() will be within
will be within ![]() of the unknown
of the unknown ![]() . Since the Synovate poll referenced by Hume (2006) resulted in
. Since the Synovate poll referenced by Hume (2006) resulted in ![]() , and
, and ![]() and
and ![]() , we can conclude that the interval from
, we can conclude that the interval from ![]() to
to ![]() likely captures (or contains)
likely captures (or contains) ![]() .
.
Confidence Interval for a Population Proportion
We just constructed an approximate 95% confidence interval for a population proportion. While 95% is a commonly-used confidence level, we could set the confidence level at any percentage between 0% and 100%. The following experiment is the general set-up for constructing a confidence interval for a proportion.
Experimental Situation
One categorical population with an unknown proportion (or percentage) ![]() .
.
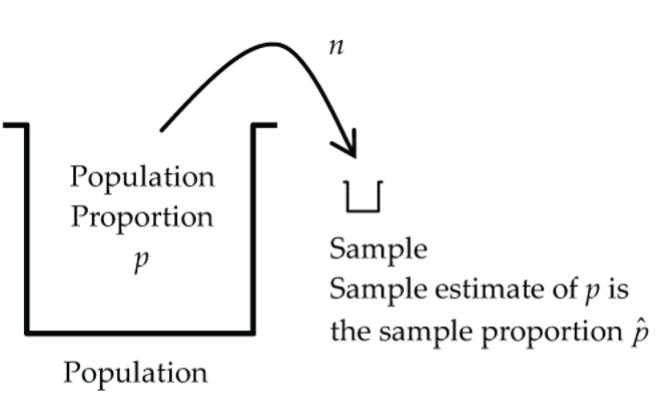
Objective
Based on the results of a random sample of ![]() observations from this population, construct a confidence interval for the unknown proportion
observations from this population, construct a confidence interval for the unknown proportion ![]() .
.
Assumptions
- Independence: The individual responses in the sample are independent of each other.
- Random: The sample is random.
- Success/Failure Condition:
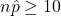 and
and 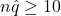 .
. - 10% Condition: The sample size
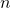 is no more than 10% of the population size.
is no more than 10% of the population size.
Confidence Interval Construction
The general form for a confidence interval for a proportion ![]() is
is ![]() , where
, where ![]() is the critical value z-score from the standard normal distribution corresponding to the specified confidence level.
is the critical value z-score from the standard normal distribution corresponding to the specified confidence level.
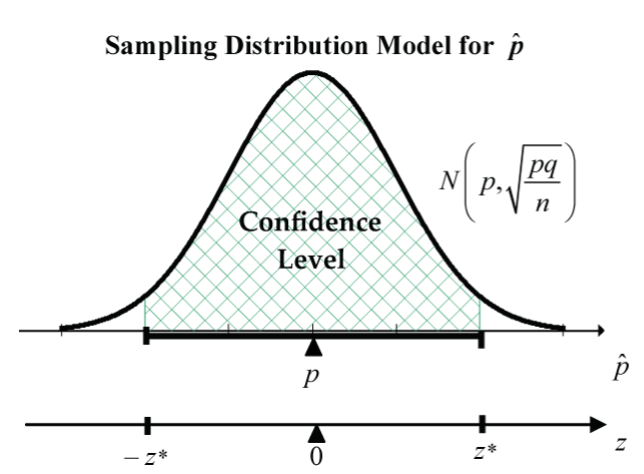
The quantity ![]() is called the margin of error of
is called the margin of error of ![]() , so the confidence interval can also be expressed as
, so the confidence interval can also be expressed as ![]() , where the margin of error is
, where the margin of error is ![]() .
.
Terminology
The standard error of ![]() is the standard deviation of
is the standard deviation of ![]() based on its sampling distribution,
based on its sampling distribution, ![]() , which we estimate by
, which we estimate by ![]() .
.
The margin of error of ![]() is the amount added to or subtracted from the point estimate,
is the amount added to or subtracted from the point estimate, ![]() , in the construction of a confidence interval for the population proportion,
, in the construction of a confidence interval for the population proportion, ![]() . It is calculated by multiplying a percentile from the normal distribution (
. It is calculated by multiplying a percentile from the normal distribution (![]() ) by the standard error of the point estimate,
) by the standard error of the point estimate, ![]() , i.e.,
, i.e., ![]() .
.
Example: Confidence Interval for a Proportion
For the next example, first consider this excerpt of a news article (Bohn, 2006) published by The Vancouver Sun.
Most Believe Afghan Mission Not Working: Poll
By Glen Bohn (2006). Adapted from The Vancouver Sun.
As with other recent public opinion polls about the three-year-old deployment, the random sample of 550 B.C. adults underlines how divided voters are about the merits of keeping Canadian soldiers in Asia. (…) A slim 53-per-cent majority of those surveyed say they support the use of Canada’s troops for security and combat efforts against the Taliban in Afghanistan….
Construct a 90% and 95% confidence interval for the proportion of BC adults that supported the use of Canada’s troops against the Taliban in Afghanistan.
Condition Check
The assumptions required for the confidence interval calculation impose conditions on this data set. Are these conditions plausible?
- Independence: Yes, individuals likely responded independently in this opinion poll.
- Random: Yes, a random sample was taken.
- Success/Failure Condition: Yes,
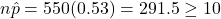 and
and  .
. - 10% Condition: Yes,
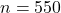 is certainly less than 10% of the BC adult population.
is certainly less than 10% of the BC adult population.
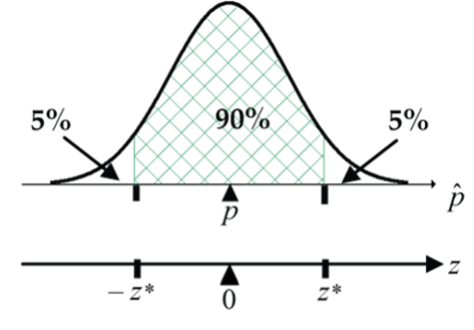
90% CI for 
In R, the code, qnorm(0.95, mean = 0, sd = 1) returns the critical z-score of 1.645, which has an area of 0.95 to the left and 0.05 to the right. You should be able to see from the diagram (Fig. 5) that the critical z-score of –1.645 has an area of 0.05 to the left and 0.95 to the right. Thus, the critical z-scores of –1.645 and 1.645 have an area of 0.90 in between.
![]() .
.
90% CI for ![]() :
: ![]() or (49.5%, 56.5%).
or (49.5%, 56.5%).
Interpretation: We are 90% confident that between 49.5% and 56.5% of adults in BC supported the use of Canada’s troops against the Taliban in Afghanistan.
95% CI for 
In R, the code, qnorm(0.975, mean = 0, sd = 1) returns the critical z-score of 1.96, which has an area of 0.975 to the left and 0.025 to the right. You should be able to see from the diagram (Fig. 6) that the critical z-score of –1.96 has an area of 0.025 to the left and 0.975 to the right. Thus, the critical z-scores of –1.96 and 1.96 have an area of 0.95 in between.

![]() .
.
95% CI for ![]() :
: ![]() or (48.8%, 57.2%).
or (48.8%, 57.2%).
Interpretation: We are 95% confident that between 48.8% and 57.2% of adults in BC supported the use of Canada’s troops against the Taliban in Afghanistan.
When you increase the confidence level from 90% to 95%, the price you pay for greater confidence is a wider interval! The 68–95–99.7 rule gives us ![]() , which is just a rounded version of the more accurate value of
, which is just a rounded version of the more accurate value of ![]() for 95% confidence.
for 95% confidence.
Interpreting a Confidence Interval for a Proportion
Usually, constructing a confidence interval for a proportion is fairly straightforward, but correctly interpreting the interval can be tricky, particularly in the use of the word “confidence” (correct) vs “probability” (incorrect). The following simulation will provide us with greater insight into the correct interpretation of a confidence interval.
Imagine we have taken a random sample from a population in which ![]() and we calculated the sample proportion to be 0.42 and a 95% confidence interval for
and we calculated the sample proportion to be 0.42 and a 95% confidence interval for ![]() to be from 0.32 to 0.52. Now imagine taking another random sample, but this time getting a sample proportion of 0.51 and a 95% confidence interval for
to be from 0.32 to 0.52. Now imagine taking another random sample, but this time getting a sample proportion of 0.51 and a 95% confidence interval for ![]() going from 0.41 to 0.61.
going from 0.41 to 0.61.
Then let’s keep going. Figure 6 illustrates what the first seven samples might look like:
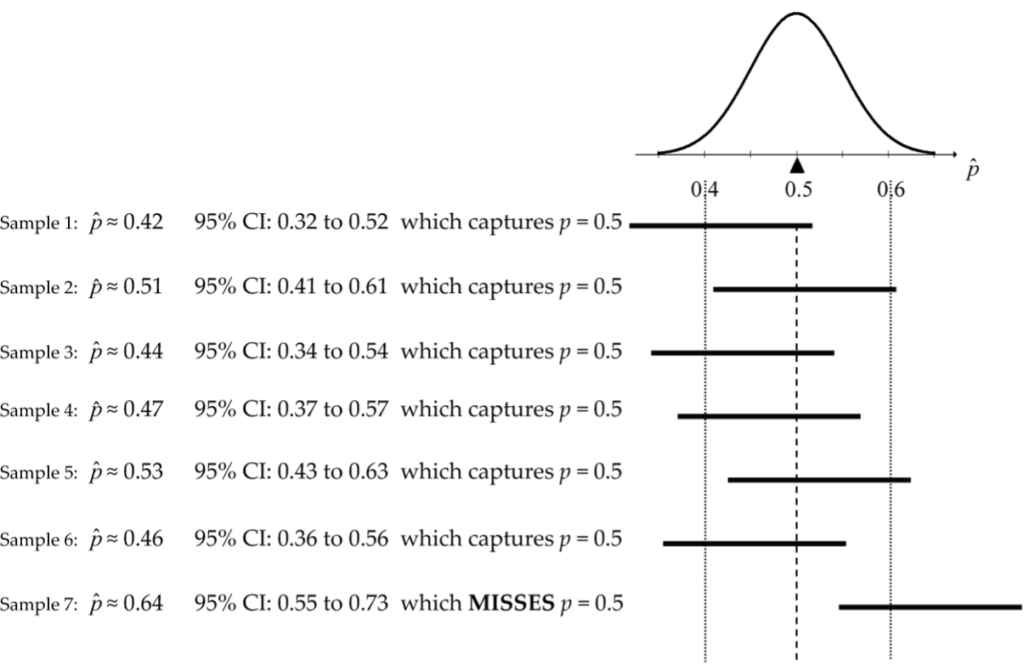
If we were to continue this process of generating 95% confidence intervals, we know that in the long run 95% of them will capture ![]() , and that’s the sense in which we are “95% confident” in any particular CI. However, it is wrong to say that any particular CI has a 95% probability of capturing
, and that’s the sense in which we are “95% confident” in any particular CI. However, it is wrong to say that any particular CI has a 95% probability of capturing ![]() . Why? Nothing is random once the sample has actually been taken. For example, the probability that the first CI from 0.32 to 0.52 captures
. Why? Nothing is random once the sample has actually been taken. For example, the probability that the first CI from 0.32 to 0.52 captures ![]() is 100% (not 95%), and the last CI of 0.55 to 0.73 has 0% probability of capturing
is 100% (not 95%), and the last CI of 0.55 to 0.73 has 0% probability of capturing ![]() .
.
When interpreting a 95% confidence interval, we say: “We are 95% confident that …” not “There is a 95% probability that ….”
References
Bohn, G. (2006, November 11). Most believe Afghan mission not working: poll. The Vancouver Sun [Excerpt]. https://advance.lexis.com/api/document?collection=news&id=urn:contentItem:4M9X-SPX0-TWD4-02G1-00000-00&context=1516831
Hume, M, (2006, November 9). A whale of support for aquarium expansion. The Globe and Mail [Excerpt]. https://www.theglobeandmail.com/news/national/a-whale-of-support-for-aquarium-expansion/article4112688/

