Lesson 2.2: Conditional Probability

Supplementary Notes 2.2

Probability Trees and Conditional Probability

The following example sets up the General Multiplication Rule for calculating the probability of two outcomes or events in a very natural way.

Example

Randomly select two balls (without replacement) from the pot in the following diagram (Fig. 1).

Urn with two black balls and three white balls
Figure 1: Container diagram with two black balls and three white balls. Two balls are removed.

Find the probability that both balls selected are black.

Solution strategy: Draw a probability tree!
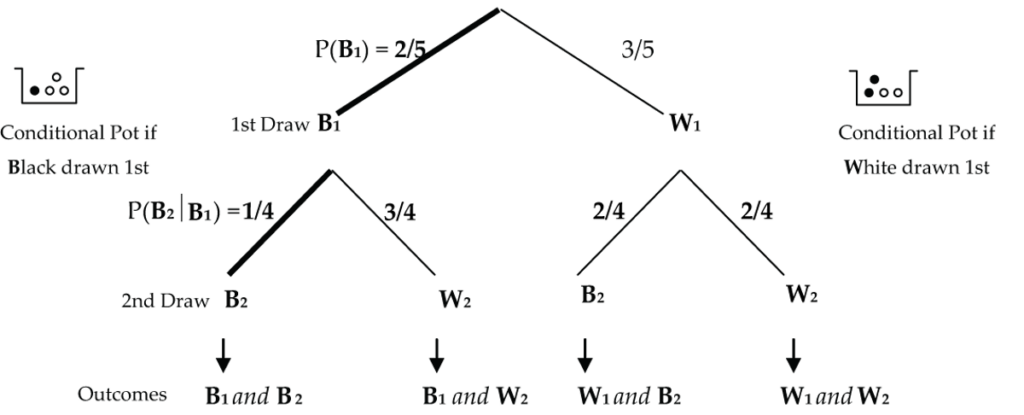
Probability tree example
Figure 2: Probability tree determines the likelihood that the two balls removed from the container (Fig. 1) are black. 

To have both balls black, we must get a black ball on the first draw (2/5 probability) and a black ball on the second draw (1/4 probability if we know that the first ball selected was black). We then just multiply these probabilities to find the probability that both balls selected are black: P(B1 and B2) = (2/5) x (1/4) = 2/20 = 1/10 = 0.1 = 10%.

Symbolically, P(B1 and B2) = P(B1) x P(B2 | B1).

The notation P(B2 | B1) means P(B2 given B1), i.e., the probability of getting a black ball on the second draw given that we got a black ball on the first draw. This is called a conditional probability.

Here, P(B2 | B1) = 1/4 because if a black ball is selected first, there are only 4 balls left in the conditional pot with 1 black and 3 whites.

“P(B1 and B2) = P(B1) x P(B2 | B1)” is the General Multiplication Rule as it applies to this question.

With a probability tree diagram, you multiply the probabilities as you travel down the “branches” of the tree. As an additional example, the probability that both balls are white is P(W1 and W2) = P(W1) x P(W2 | W1) = (3/5) x (2/4) = 6/20 = 3/10 = 0.3 = 30%.

General Multiplication Rule

For any two events A and B: P(A and B) = P(A) x P(B | A).

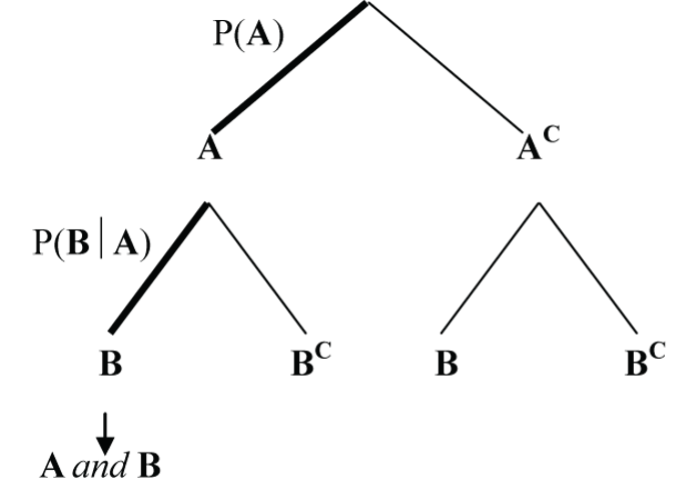
General probability tree for two events
Figure 3: Probability tree for two events

Independence

Two events A and B are independent if P(B | A) = P(B).

This is the formal definition of independence. In words it says that two events are independent if the occurrence of one event does not alter the probability of the other event occurring. If events A and B are independent,  then P(B | A) = P(B) and the General Multiplication Rule simplifies to P(A and B) = P(A) x P(B), which is the Multiplication Rule for Independent Events from Lesson 2.1: Probabilities of Events.

Example

Consider an experiment with 12 male and 13 female patients. If two subjects are randomly selected from the 25 (without replacement), find the probability that:

  1. Both are male.
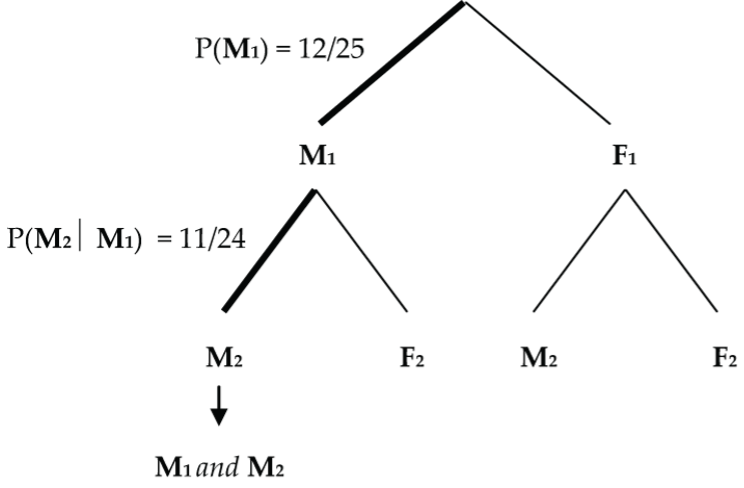
    Probability tree example
    Figure 4: Probability tree determines the likelihood that two randomly-selected participants are male

     

    P(M1 and M2) = P(M1) x P(M2 | M1) = (12/25) x (11/24) = 132/600 = 22/100 = 0.22 = 22%.

  2. At least one of the two is female.
    P(at least one female) = 1 – P(no females) = 1 – P(M1 and M2) = 1 – 0.22 = 0.78 = 78%.

Example: General Multiplication Rule

Consider an experiment with three treatment levels (physio, drug, and sham/control), in which 8 patients received physio, 11 patients received drug, and 6 patients received sham/control. If two subjects are randomly selected from the 25 patients (without replacement), find the probability that they both receive the same treatment.

Ph = Physio, D = Drug, S = Sham/control
Decision tree example
Figure 5: Probability tree determines the likelihood that two randomly-selected participants receive the same treatment. 

 

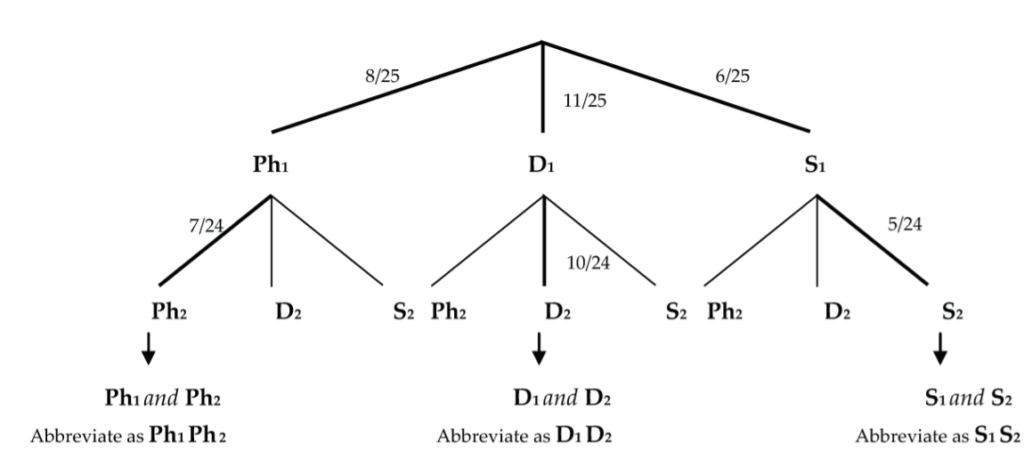
P((Ph1 and Ph2) or (D1 and D2) or (S1 and S2)) = (P(Ph1) x P(Ph2 | Ph1)) + (P(D1) x P(D2 | D1)) + (P(S1) x P(S2 | S1)) = ((8/25) x (7/24)) + ((11/25) x (10/24)) + ((6/25) x (5/24)) = 196/600 = 0.3267 = 32.67%.

We use the General Multiplication Rule to calculate P(Ph1 and Ph2), P(D1 and D2), and P(S1 and S2).

The outcomes (Ph1 and Ph2), (D1 and D2), and (S1 and S2) are disjoint since they can’t happen simultaneously. So, we use the Addition Rule for Disjoint Events from Lesson 2.1: Probabilities of Events to add their probabilities.

So, there is a 32.67% chance that both subjects will receive the same treatment.

Additional Examples

Example 1

In 2 spins of the pointer below (Fig. 6), find the probability that the $5 outcome comes-up only once.

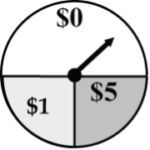
Pointer arrow spins within a circle to select various amounts of money. Half of the circle is labelled zero dollars, a quarter of the circle is labelled one dollar, and the other quarter of the circle is labelled five dollars. The arrow is currently pointing at zero dollars.  
Figure 6: A pointer arrow spins within a circle to select various amounts of money.
Since the question only asks about $5 outcomes, we don’t need to keep track of $0 or $1 outcomes separately in our tree diagram, only F = $5 and FC = {$0, $1}.

 

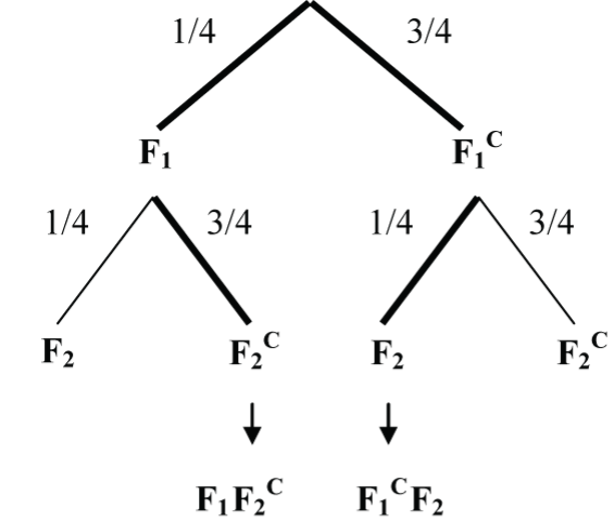
Probability tree example
Figure 7: Probability tree determines the likelihood that the 5 dollar outcome comes-up only once in two spins of the pointer (Fig. 6)
Notice that in this tree diagram (Fig. 7), the probabilities on the branches of the tree stay the same (1/4 and 3/4) for each spin. This means that the trials (spins) are independent and we can use the Multiplication Rule for Independent Events. Compare this to the previous example where the branch probabilities changed on the second draw because the subjects were being removed, and the trials (draws) were dependent.

P((F1 and F2C) or (F1C and F2)) = (P(F1) x P(F2C)) + (P(F1C) x P(F2)) = ((1/4) x (3/4)) + ((3/4) x (1/4)) = 6/16 = 0.375 = 37.5%.

So, there is a 37.5% chance that the $5 comes up only once.

Example 2

Consider the sample space S below (Fig. 8):

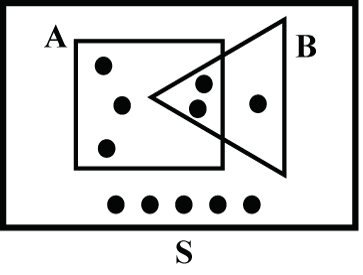
Sample space example
Figure 8: Sample space S has 11 black dots. A square (A) and triangle (B) shape overlap. Five dots are within shape A; three dots are within shape B; and two of these dots are in both A and B. Five additional dots are below the shapes. 

If each of the 11 outcomes in the sample space S are equally likely, then we can count the dots to get: P(A) = 5/11, P(B) = 3/11, P(A and B) = 2/11, and P(A or B) = 6/11.

Notice that A and B are not disjoint because they have two outcomes in common.

P(B | A) = 2/5.

“Given A” means that only the 5 dots in A are possible, and 2 of these 5 dots are also in B.

Are events A and B independent?

No, since P(B | A) = 2/5 \neq P(B) = 3/11.

Can we use the General Multiplication Rule to calculate P(A and B)?

Of course (although it is much easier in this case to just count the dots as above): P(A and B) = P(A) x P(B | A) = (5/11) x ( 2/5) = 2/11.

Other conditional probabilities: P(A | B) = 2/3, P(A | BC) = 3/8, P(B | AC) = 1/6. Make sure you can derive each of these from the sample space S above.

Example: Independence

Consider 200 students’ movie preferences in the following contingency table (Table 1).

Table 1 Student Movie Preference Contingency Table
Movie Preferences
Drama Action Comedy
Male 20 a b 120
Female 40 c d 80
60 100 40 200
  1. For these 200 students, are the events “student is male” and “student prefers drama” independent?
    • M = Student is male
    • D = Student prefers drama

    For M and D to be independent, we must have P(M | D) = P(M).Here P(M | D) = 20/60 = 1/3, and P(M) = 120/200 = 3/5.

    Since P(M | D)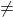 \neq P(M), we conclude that M and D are not independent––they are dependent.

    This question could also have been answered by seeing if P(D | M) = P(D).

    Here P(D | M) = 20/120 = 1/6, and P(D) = 60/200 = 3/10.

    Since P(D | M) \neq P(D), we conclude that M and D are not independent––they are dependent.
  2. Fill-in the missing entries in Table 1 in such a way that the two events M = “Student is male” and C = “Student prefers comedy” are independent. For M and C to be independent, we must have P(M | C) = P(M). So b/40 = 120/200, b = (120/200) x 40 = 24. By subtraction, we get d = 16, a = 76, c = 24.

Let’s step back and interpret these results in context.

Part 1 of this example is saying that only 1/3 of those people preferring drama are males, yet males make up 3/5 = 60% of this entire group, so there is an association between “drama preference” and “male.” They are dependent.

Part 2 is saying that 24/40 = 3/5 = 60% of those people preferring comedy are males, which is exactly equal to the percentage of males in the entire group, so there is no association between “comedy preference” and “male.” They are independent.

Conditional Probability Revisited

So far, the calculation of a conditional probability like P(A | B) or P(B | A) has come naturally by direct count or evaluation. Most of the time this will be the case, but there are some applications where a conditional probability can’t be calculated this way and we need a formula to calculate it. Which formula? It’s just the General Multiplication Rule rearranged.

General Multiplication Rule: P(A and B) = P(A) x P(B | A) = P(B | A) x P(A).

Note that by considering events A and B in the opposite order, the General Multiplication Rule can also be expressed as P(A and B) = P(B and A) = P(B) x P(A | B) = P(A | B) x P(B).

Therefore, we can write P(A | B) x P(B) = P(B | A) x P(A).

And so P(A | B) = P(B | A) x P(A) / P(B).

Next, write P(B) = P((A and B) or (AC and B)) = P(A and B) + P(AC and B) = (P(B | A) x P(A)) + (P(B | AC) x P(AC)).

Then, P(A | B) = P(B | A) x P(A) / ((P(B | A) x P(A)) + (P(B | AC) x P(AC))).

This is known as Bayes Theorem.

Example: Reversing the Conditioning

Only 1 in 1,000 adults is afflicted with a rare disease for which a diagnostic test has been developed. The test is such that, when a person actually has the disease, a positive test result will occur 99% of the time, while a person without the disease will show a positive test result only 2% of the time (a so-called “false positive”). If a randomly selected person is tested and the result is positive, what is the probability that the person has the disease?

Lots of words! Let’s start by identifying the given information symbolically:

  • D = Person has disease
  • Pos = Person tests positive
Notice that the conditional probability that we are asked to find is the reverse conditioning of one of the conditional probabilities that we were given.
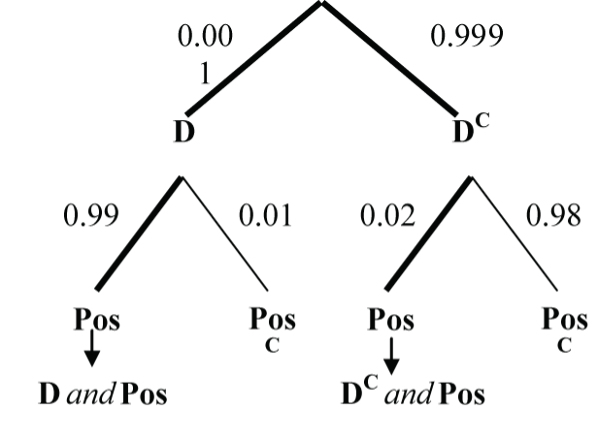
Bayes rule tree
Figure 9: Bayes rule probability tree determines if a person who tested positive has the disease.

Find P(D | Pos) given:

  • P(D) = 1/1000 = 0.001
  • P(Pos | D) = 0.99
  • P(Pos | DC) = 0.02

Since P(D | Pos) doesn’t come “naturally,” we use Bayes Theorem to calculate it.

  • P(D | Pos) = P(Pos | D) x P(D) / ((P(Pos | D) x P(D)) + (P(Pos | DC) x P(DC)))
  • P(D | Pos) = (0.99 x 0.001) / ((0.99 x 0.001) + (0.02 x 0.999))
  • P(D | Pos) = 0.0472

So, the probability that the person has the disease is only about 4.72%. Surprised that it is so low? It is low because the disease is rare, and the false positive rate is relatively high at 2%.

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Introduction to Probability and Statistics Copyright © 2023 by Thompson Rivers University is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book