Software Lab 3.3

Iain Pardoe

Lesson 3.3: Hypothesis Testing

Software Lab 3.3

Hypothesis Testing

In the last lab, we used a sample to make inferences on a population proportion by calculating a confidence interval. In this lab, we’ll come at the same question from a different, but related, perspective: hypothesis testing.

As you work through the lab, answer the ungraded exercises in the shaded boxes. Check your answers by consulting the Software Lab 3.3 Solutions.

Remember to complete the graded Software Lab Questions for this section in Moodle.

Getting Started

The Data

We’ll use the same scenario as in the last lab: a total population size of 100,000 US adults, with 62,000 (62%) of those adults thinking that climate change impacts their community, and the remaining 38,000 thinking that climate change does not impact their community.

The name of the data frame is us_adults and the name of the variable that contains responses to the question “Do you think climate change is affecting your local community?” is climate_change_affects. The file representing the entire population can be found at us_adults [CSV file] (OpenIntro, n.d.).

In this lab, you’ll again work with a simple random sample of size 60 from this population. Create a new computed variable named sample1 using the formula SAMPLE(climate_change_affects,60). You’ll use this sample to make inferences on the population proportion using hypothesis testing. In this case, we have the rare luxury of knowing the true population proportion ( $p=62\%$ ) since we have data on the entire population. So, you’ll be able to use this knowledge to learn about the properties of the hypothesis testing procedure.

Hypothesis Test for a Proportion

1. State the null and alternative hypotheses to test. Does your sample have sufficient evidence to conclude whether the proportion of adults in the population that think climate change affects their local community is different from 62%? Check your answer by consulting the Software Lab 3.3 Solutions.

2. Check the conditions needed for the normal model in this one-proportion context.

3. Select Analyses > Exploration > Descriptives to create a frequency table for the sample1 variable to calculate the sample proportion of US adults that think climate change affects their local community, 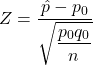$\hat{p}$ . Then use $\hat{p}$ from your sample and $p_0=0.62$ to calculate the test statistic, $Z = \dfrac{\hat{p}-p_0}{\sqrt{\dfrac{p_0q_0}{n}}}$ .

4. Select Analyses > R > Rj Editor and use the R function pnorm to calculate the p-value corresponding to the test statistic from the previous question. Hint: Review Example 2: One-Proportion Z-Test about the Green Party in Supplementary Notes 3.3.

5. Use the p-value from question 4 to evaluate the hypothesis test; i.e., determine whether or not to reject the null hypothesis in favour of the alternative hypothesis based on a significance level $\alpha = 0.05$ .

6. Draw a conclusion in the context of the problem based on your answer to question 5; i.e., state whether there is sufficient evidence in your sample that the proportion of adults in the population that think climate change affects their local community is different from 62%.

Hypothesis Test Errors

Type 1 Error and the Significance Level

If we take multiple simple random samples of size 60 from the population, each sample would result in a slightly different sample proportion, $\hat{p}$ , and hence a slightly different test statistic, $Z$ , and p-value. Some of those p-values would be greater than the significance level $\alpha = 0.05$ , resulting in not rejecting the null hypothesis. This would be a correct decision since in this case we know the population proportion is 62%.

7. On the other hand, some of those p-values would be less than $\alpha = 0.05$ , resulting in rejecting the null hypothesis in favour of the alternative hypothesis. This would be an incorrect decision and lead to a Type 1 error. In what proportion of the repeated simple random samples would this happen (getting a p-value less than $\alpha = 0.05$ )?

8. Use Errors and Power [Application] (CPM Educational Program, 2023) to gain some insight into the previous question. Set the null hypothesis to $p_0 = 0.62$ , the alternative hypothesis to $p \ne p_0$ , the sample size to $n = 60$ , and the significance level to $\alpha = 0.05$ . Don’t worry about the “suspected true population proportion” yet, so leave that set to 0.5. Then, select “Type I Error” to shade this area probability in the tails of the null distribution. This probability is reported at the top of the screen as “P(Type I Error).” Does this probability match your answer to the previous question? Explain.
Note: Hypothesis errors are referred to as Type 1 and Type 2 in the textbook, but Type I and Type II in the Errors and Power app.

Type 2 Error and Power

Suppose your sample didn’t come from a population in which the proportion was 62%, but instead came from a population in which the proportion was 80%. Now, a correct decision would be to reject the null hypothesis in favour of the alternative hypothesis. An incorrect decision would be to not reject the null hypothesis, which would lead to a Type 2 error.

9. In the Errors and Power [Application] (CPM Educational Program, 2023), leave the null hypothesis set to $p_0 = 0.62$ , the alternative hypothesis set to $p \ne p_0$ , the sample size set to $n = 60$ , and the significance level set to $\alpha = 0.05$ , but change the “suspected true population proportion” from 0.5 to 0.8 (i.e., 80%). Then select “Type II Error” and “Power” to shade these area probabilities in the tails of the true (suspected) distribution. State these probabilities, which are reported at the top of the screen as “P(Type II Error)” and “Power.”

10. What happens to P(type 1 error), P(type 2 error), and power if you increase the sample size to 100 (and leave the other settings fixed) in the Errors and Power app?

References

CPM Educational Program. (2023). Errors and power [Application]. https://stats.cpm.org/power/

OpenIntro. (n.d.-b). us_adults [Data set]. https://github.com/OpenIntroStat/oilabs-jamovi/raw/main/05b_confidence_intervals/more/us_adults.csv

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Introduction to Probability and Statistics Copyright © 2023 by Thompson Rivers University is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.