Software Lab 5.1

Iain Pardoe

Lesson 5.1: Inference for One Mean or a Mean Difference from Two Paired Groups

Software Lab 5.1

One-Sample t-Tests and t-Intervals

As you work through the lab, answer the ungraded exercises in the shaded boxes. Check your answers by consulting the Software Lab 5.1 Solutions.

Remember to complete the graded Software Lab Questions for this section in Moodle.

Getting Started: The Data

The National Center of Education Statistics conducted a survey of high school seniors, collecting test data on reading, writing, and several other subjects. Here we examine a simple random sample of 200 students from this survey. The name of the data frame for this lab is hsb2 and the variables we’ll be using in this lab are:

math: standardized math score
science: standardized science score

Download the data from hsb2 [CSV file] (OpenIntro, n.d.), and open it in jamovi. Before we start to analyze the data, we need to change the variable types from “nominal” to “continuous.” Go to the Data tab and double-click the header for the math column. Change “Measure type” to “Continuous.” Repeat for science.

Confidence Interval for a Mean

First, we’ll focus on the variable math to make inferences about the standardized math scores for high school seniors. A confidence interval for a mean based on a t-model with n − 1 df is: $\overline{y} \pm t^* \times SE(\overline{y})$ , where $SE(\overline{y}) = \dfrac{s}{\sqrt{n}}$ , assuming the following conditions are satisfied:

The individual responses in the sample are independent of each other.
The sample is random.
The sample size 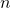$n$ is no more than 10% of the population size.
The data come from a population that is nearly normal.

1. Select Analyses > T-Tests > One Sample T-Test, move math to the Dependent Variables box, and under “Assumption Checks” click “Q–Q Plot.” Use the plot and any other relevant information to check the nearly normal condition. Check your answer by consulting the Software Lab 5.1 Solutions.

2. Still in the “One Sample T-Test” dialog, under “Additional Statistics” click “Mean difference,” “Confidence interval,” and “Descriptives.” Confirm the calculation of the 95% confidence interval for the mean using the sample statistics. Hint: Your calculation may not match the jamovi output for the interval exactly due to rounding error. Find the value of $t^*$ by selecting R > Rj Editor and running the following code: qt(0.975, df=199).

3. Interpret the interval in the context of the problem.

Hypothesis Test for a Mean

A university admissions officer has been told that the mean standardized math score for high school seniors is 55, but the admissions officer doesn’t believe this. We’ll conduct a two-sided hypothesis test for a mean to test the admissions officer’s belief. The hypotheses are H₀: µ = 55 versus H_A: µ ≠ 55. When the conditions above are met, $t=\dfrac{\overline{y}-\mu_0}{SE(\overline{y})}$ follows a t-model with n − 1 df.

4. Still in the “One Sample T-Test” dialog, under “Hypothesis” type “55” into the box for “Test value” and make sure “≠ Test value” is selected for the (alternative) hypothesis. Confirm the calculation of the test statistic using the sample statistics and calculate the p-value. Hint: Your calculation may not match the jamovi output for the test statistic exactly due to rounding error. Find the p-value by selecting R > Rj Editor and running the following code: 2*pt(-3.55, df=199).

5. Evaluate the hypothesis test from question 4 based on a significance level $\alpha = 0.05$ and draw a conclusion in the context of the problem.

Confidence Interval for a Mean Difference for Paired Data

Next, we’ll consider whether there is a difference in the mean scores of students for math and science.

6. Select Analyses > T-Tests > Paired Samples T-Test, move math and science to the Paired Variables box, and under “Assumption Checks” click “Q–Q Plot.” Use the plot and any other relevant information to check the nearly normal condition.

7. Still in the “Paired Samples T-Test” dialog, under “Additional Statistics” click “Mean difference” and “Confidence interval.” Confirm the calculation of the 95% confidence interval for the mean difference using the “Mean difference,” “SE difference,” and the appropriate value of $t^*$ . Hint: Your calculation may not match the jamovi output for the interval exactly due to rounding error. Use the same value of $t^*$ from question 2.

8. Interpret the interval in the context of the problem.

Hypothesis Test for a Mean Difference for Paired Data

The university admissions officer thinks that the mean standardized math score for high school seniors differs from the mean standardized science score. We’ll conduct a two-sided hypothesis test for a mean to test the admissions officer’s belief. The hypotheses are H₀: µ_math = µ_science versus H_A: µ_math ≠ µ_science.

9. Still in the “Paired Samples T-Test” dialog, under “Hypothesis” make sure “Measure 1 ≠ Measure 2” is selected for the (alternative) hypothesis. Confirm the calculation of the test statistic using the “Mean difference” and “SE difference” and calculate the p-value. Hint: Your calculation may not match the jamovi output for the test statistic exactly due to rounding error. Find the p-value by selecting R > Rj Editor and running the following code: 2*(1-pt(1.36, df=199)).

10. Evaluate the hypothesis test from question 9 based on a significance level $\alpha = 0.05$ and draw a conclusion in the context of the problem.

References

OpenIntro. (n.d.). Data sets [Data sets]. https://openintro.org/data/

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Introduction to Probability and Statistics Copyright © 2023 by Thompson Rivers University is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.