Lesson 5.2: Inference for Difference in Means from Two Independent Groups
Software Lab 5.2
Two-Sample t-Tests and t-Intervals
Part of this software lab is adapted from Inference for Numerical Data (OpenIntro, n.d.-b) CC BY-SA 4.0.
As you work through the lab, answer the ungraded exercises in the shaded boxes. Check your answers by consulting the Software Lab 5.2 Solutions.
Remember to complete the graded Software Lab Questions for this section in Moodle.
North Carolina Births: The Data
Download ncbirths150 [CSV file] (OpenIntro, n.d.-a) and load it into jamovi. This dataset is a random sample of 100 births for babies in North Carolina where the mother was not a smoker and another 50 where the mother was a smoker. This dataset is analyzed in Section 7.3.2 in the textbook. The variables we’ll be using in this lab are:
weight: birth weight of the babysmoke: whether or not the mother was a smoker
Hypothesis Test for the Difference of Two Independent Means
Is there convincing evidence that newborns from mothers who smoke have a different average birth weight than newborns from mothers who don’t smoke? We’ll conduct a two-sided hypothesis test for the difference of two independent means to answer this question.
The hypotheses are H0: µ1 − µ2 = 0 versus HA: µ1 − µ2 ≠ 0 (µ1 is the mean for the nonsmoker group, µ2 is the mean for the smoker group). The test statistic 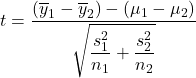 can be modeled by Student’s t-model with degrees of freedom given by
can be modeled by Student’s t-model with degrees of freedom given by 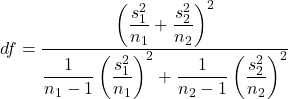 , assuming the following conditions are satisfied:
, assuming the following conditions are satisfied:
- Independence Between Groups: The two groups that we are comparing are independent of each other. This means that there is no linkage or association between the two groups. This would be the case in a completely randomized experiment where the two groups are formed at random, but it would not be the case if we used twin pairs, for example, to form the two groups.
- Independence Within Groups: Within each group, the individual measurements are independent of each other.
- Random: Each of the two samples is randomly drawn from their respective populations.
- Nearly Normal Condition: For each of the two samples, the data come from a population that is nearly normal. This condition is important for small data sets, but if each sample is relatively large (say > 30), we don’t have to worry about it too much.
- 10% Condition: Each of the two sample sizes, n1 and n2, is no more than 10% of their respective population sizes.
Analyses > T-Tests > Independent Samples T-Test, move weight to the Dependent Variables box, move smoke to the Grouping Variable box, and under Tests select Welch's. Unselect Student's if it is selected already. Also, under Additional Statistics select Mean difference. Calculate the test statistic using the “Mean difference” and “SE difference” and check it matches the value in the “Independent Samples T-Test” output (within rounding error). Hint: Your calculation won’t match the value in the textbook, since there are rounding errors in the textbook calculation. It also won’t match the value you get if you input the sample statistics into an online t-test calculator [Application] , since there are rounding errors involved with that too. Check your answer by consulting the Software Lab 5.2 Solutions.Additional Statistics select Descriptives. Use the group sample sizes and standard deviations to calculate the degrees of freedom, and check it matches the value in the “Independent Samples T-Test” output (within rounding error).R > Rj Editor and run the following code: 2*(1-pt(1.50, df=89.3)). Your calculation won’t match the value in the textbook, which uses the wrong degrees of freedom value.High-Schoolers’ Physical Activity: The Data
Download yrbss_activity [CSV file] (OpenIntro, n.d.-a) and load it into jamovi. This dataset is based on the United States’ Centers for Disease Control and Prevention Youth Risk Behavior Surveillance System (YRBSS) survey. We used data from the survey previously in Software Lab 4.1 and Software Lab 4.3.
The variables we’ll be using in this lab are:
height: self-reported height in metresweight: self-reported weight in kilogramsphysically.active.7d: days per week that the participant is physically active
After opening the data in jamovi, create the following new variables (go to the Data tab and double-click the header of the first empty column):
bmi: use formulaweight/height^2physical_3plus: use formulaIF(physically_active_7d>2,"yes","no")
Hypothesis Test for the Difference of Two Independent Means
Is there convincing evidence that high-schoolers who are physically active at least three days a week have a different average body mass index (BMI) than high-schoolers who are physically active two or fewer days a week? As with the North Carolina births example, we’ll conduct a two-sided hypothesis test for the difference of two independent means to answer this question.
Analyses > T-Tests > Independent Samples T-Test, move bmi to the Dependent Variables box, move physical_3plus to the Grouping Variable box, and under Tests select Welch's. Unselect Student's if it is selected already. Also, under Additional Statistics select Mean difference. Calculate the test statistic using the “Mean difference” and “SE difference,” and check it matches the value in the “Independent Samples T-Test” output (within rounding error).Additional Statistics select Descriptives. Use the group sample sizes and standard deviations to calculate the degrees of freedom and check it matches the value in the “Independent Samples T-Test” output (within rounding error).R > Rj Editor and run the following code: 2*pt(-4.52, df=6959).Confidence Interval for the Difference of Two Independent Means
A confidence interval for the difference of two independent means is 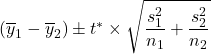 , where
, where ![]() comes from a t-distribution with degrees of freedom given above.
comes from a t-distribution with degrees of freedom given above.
Additional Statistics select Confidence interval. Confirm the calculation of the 95% confidence interval for the mean difference using the “Mean difference,” “SE difference,” and the appropriate value of R > Rj Editor and running the following code: qt(0.975, df=6959).References
OpenIntro. (n.d.-a). Data sets [Data sets]. https://openintro.org/data/
OpenIntro. (n.d.-b) CC BY-SA 4.0. Inference for numerical data. OpenIntro Labs for jamovi. https://openintrostat.github.io/oilabs-jamovi/07_inf_for_numerical_data/inf_for_numerical_data.html
Statistics Kingdom. (n.d.). Two sample t-test calculator (Welch’s t-test) [Application]. https://www.statskingdom.com/150MeanT2uneq.html

