Lesson 2.1: Probabilities of Events
Software Lab 2.1 Solutions
- A 6 was rolled 1,676 times. The number rolled the fewest times was 4, with a count of 1,650.
- The proportion of die rolls in event B is (1,650+1,676) / 10,000 = 3,326 / 10,000 = 0.3326.
- The proportion of die rolls in event A or event B is (1,671+1,680+1,650+1,676) / 10,000 = 6,677 / 10,000 = 0.6677. The sum of the proportion of die rolls in event A and the proportion of die rolls in event B is 0.3351 + 0.3326 = 0.6677.
- The proportion of die rolls in event A or event D is (1,671+1,680+1,666) / 10,000 = 5,017 / 10,000 = 0.5017. The sum of the proportion of die rolls in event A and the proportion of die rolls in event D is 0.3351 + (1,680+1,666) / 10,000 = 0.3351 + 0.3346 = 0.6697.
- The proportion of times event A occurred was (2,498+2,509)/ 10,000 = 5,007 / 10,000 = 0.5007.
- The proportion of times the card was black was (2,490+2,503)/ 10,000 = 4,993 / 10,000 = 0.4993. Alternatively, using the complement of event A, the proportion of times the card was black was 1 – 0.5007 = 0.4993.
- The card was a queen of hearts 190 times.
- The product of the proportion of times the card was a queen and the proportion of times the card was a heart is 0.0761 x 0.2509 = 0.0191, which is close to the proportion of times the card was the queen of hearts, 0.0190.
- P(A) x P(B) = 3/13 x 2/13 = 6/169
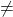P(A and B) = 4/13. - The product of the proportion of times the card was a face card and the proportion of times the card was a king or an ace is (0.0787+0.0761+0.0770) x (0.0770+0.0762) = 0.2318 x 0.1532 = 0.0355, which is not close to the proportion of times the card was a jack, a queen, a king, or an ace, (0.0787+0.0761+0.0770+0.0762) = 0.3080.
