Lesson 3.2: Confidence Intervals
Software Lab 3.2 Solutions
- Answers will vary, but on average should be close to 62%.
- The sample proportion from another sample will generally not be identical, but should be somewhat similar since these are simple random samples of a reasonable size from the same population.
- Answers will vary, but if
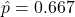 , say, then
, say, then 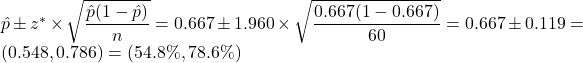 .
. - Answers will vary, but likely yes. The interval for
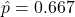 was calculated to be
was calculated to be 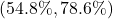 , so this interval does contain the true population proportion,
, so this interval does contain the true population proportion, 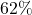 .
. - 95% of those intervals would be expected to contain the true population proportion since this property follows from how confidence intervals are constructed.
- Answers will vary, but likely close to 0.95 or 95%. The proportion could differ from 0.95 since the samples are drawn randomly and the proportion only matches the confidence level “on average” (i.e., for an “infinite” number of samples).
- A 90% confidence interval is narrower than a 95% confidence interval (all else equal) because we can narrow the range of values if we’re less confident the interval contains the population proportion.
- Answers will vary, but if
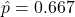 , say, then
, say, then 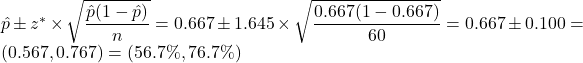 . This 90% interval is narrower than the 95% interval from question 3.
. This 90% interval is narrower than the 95% interval from question 3. - Answers will vary, but likely close to 0.90 or 90%, the confidence level of the intervals.
- A 99% confidence interval is wider than a 95% confidence interval (all else equal). If
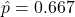 , say, then
, say, then 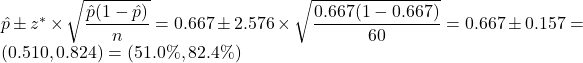 .
.

