Lesson 4.1: Inference for Proportions
Software Lab 4.1 Solutions
-
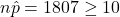 and
and 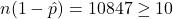 .
.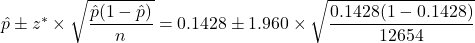
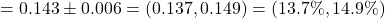 .
.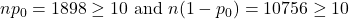 .
.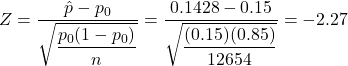 .
.- R code
2 * pnorm(-2.27, mean=0, sd=1)returns the p-value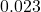 . Since
. Since 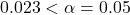 , reject H0 in favour of HA and conclude that there is sufficient evidence in the sample that the proportion of US high-schoolers who texted while driving for six or more days over the preceding 30 days is different from 15%. The survey results suggest that the proportion of US high-schoolers who texted while driving for six or more days over the preceding 30 days is less than 15%.<
, reject H0 in favour of HA and conclude that there is sufficient evidence in the sample that the proportion of US high-schoolers who texted while driving for six or more days over the preceding 30 days is different from 15%. The survey results suggest that the proportion of US high-schoolers who texted while driving for six or more days over the preceding 30 days is less than 15%.< 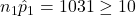 ,
, 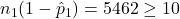 ,
, 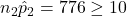 , and
, and 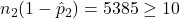 .
.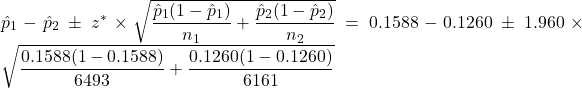
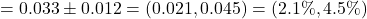 .
.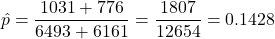 .
. 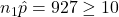 ,
, 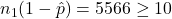 ,
, 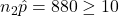 , and
, and 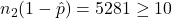 .
.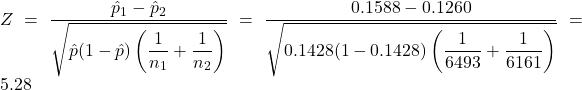 .
.- R code
2 * (1 - pnorm(5.28, mean=0, sd=1))returns the p-value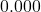 . Since
. Since 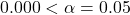 , reject H0 in favour of HA and conclude that there is sufficient evidence in the sample that the population proportions US high-schoolers who have texted while driving for six or more days over the preceding 30 day are not equal for males and females. The survey results suggest that the proportion of US high-schoolers who texted while driving for six or more days over the preceding 30 days is higher for males than females.
, reject H0 in favour of HA and conclude that there is sufficient evidence in the sample that the population proportions US high-schoolers who have texted while driving for six or more days over the preceding 30 day are not equal for males and females. The survey results suggest that the proportion of US high-schoolers who texted while driving for six or more days over the preceding 30 days is higher for males than females.

