Lesson 4.3: Testing Independence in Two-way Tables

Software Lab 4.3 Solutions

  1. The expected frequencies for green/left and other/left are 3.83 and 2.67, respectively, so they are not all at least five.
  2. The expected frequencies are now all at least five.
  3. The test statistic in the jamovi test output is 0.708, and the p-value is 0.702:
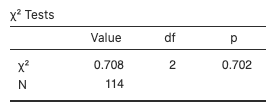
    jamovi-chi-square-independence
    Figure 1: Chi-square test for independence 
  4. The observed frequencies are:
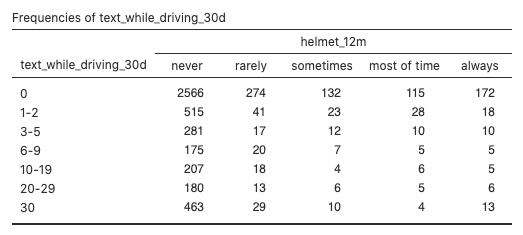
    observed frequencies
    Figure 2: Observed frequencies (never, rarely, sometimes, most of time, always) of the text_while_driving_30d variable
  5. The expected frequencies are all at least five:
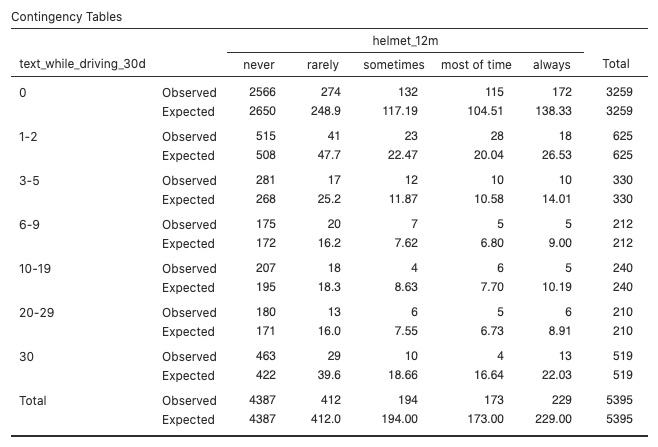
    observed and expected frequencies
    Figure 3: Contingency table shows observed and expected frequencies (never, rarely, sometimes, most of time, always) for text_while_driving_30d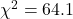
  6. \chi^2 = 64.1.
  7. Degrees of freedom = (7 − 1)(5 − 1) = 6 x 4 = 24, which matches the value in the jamovi output.
  8. p-value < 0.001.
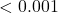  9. Since p-value 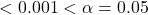< 0.001 < \alpha = 0.05, there is sufficient evidence to reject the null hypothesis. The data do not support the claim that the variables text_while_driving_30d and helmet_12m are independent.
  10. The following combinations have the largest standardized differences between observed and expected frequency, \dfrac{Obs-Exp}{\sqrt{Exp}}.
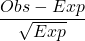    More than expected: high-schoolers who always wore a helmet and never texted while driving (172 observed, 138.33 expected). Fewer than expected: high-schoolers who never wore a helmet and never texted while driving (2,566 observed, 2,650 expected).
    More than expected: high-schoolers who never wore a helmet and texted every day while driving (463 observed, 422 expected). Fewer than expected: high-schoolers who wore a helmet most of the time and texted every day while driving (4 observed, 16.64 expected).
    R can do the necessary calculations to find the largest standardized differences between observed and expected frequency,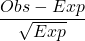 \dfrac{Obs-Exp}{\sqrt{Exp}}, with the following code (use Analyses > R > Rj Editor to run this code in jamovi):
    x <- c(2566,274,132,115,172,515,41,23,28,18,281,17,12,10,10,175,20,7,5,5,207,18,4,6,5,180,13,6,5,6,463,29,10,4,13)
    obs <- t(matrix(x, nrow=5))
    test <- chisq.test(obs, correct=FALSE)
    round(test$residuals, 1)

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Introduction to Probability and Statistics Copyright © 2023 by Thompson Rivers University is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book