Lesson 2.2: Conditional Probability
Supplementary Notes 2.2
Probability Trees and Conditional Probability
The following example sets up the General Multiplication Rule for calculating the probability of two outcomes or events in a very natural way.
Example
Randomly select two balls (without replacement) from the pot in the following diagram (Fig. 1).

Find the probability that both balls selected are black.
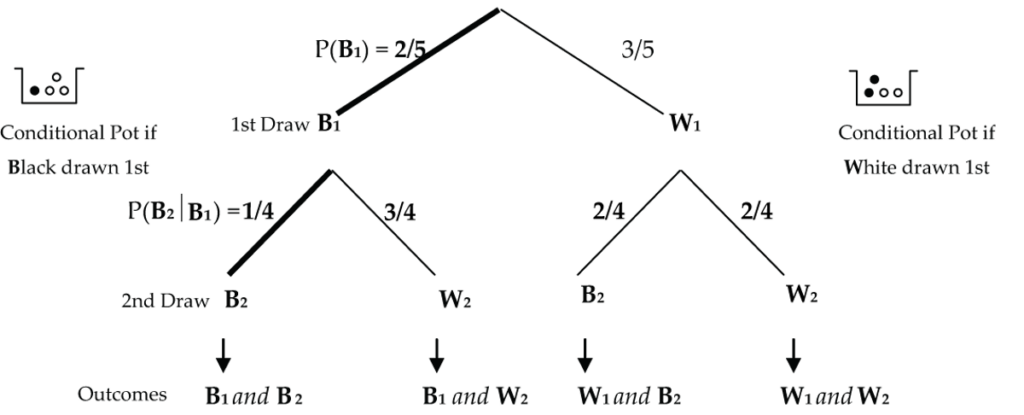
To have both balls black, we must get a black ball on the first draw (2/5 probability) and a black ball on the second draw (1/4 probability if we know that the first ball selected was black). We then just multiply these probabilities to find the probability that both balls selected are black: P(B1 and B2) = (2/5) x (1/4) = 2/20 = 1/10 = 0.1 = 10%.
Symbolically, P(B1 and B2) = P(B1) x P(B2 | B1).
The notation P(B2 | B1) means P(B2 given B1), i.e., the probability of getting a black ball on the second draw given that we got a black ball on the first draw. This is called a conditional probability.
Here, P(B2 | B1) = 1/4 because if a black ball is selected first, there are only 4 balls left in the conditional pot with 1 black and 3 whites.
“P(B1 and B2) = P(B1) x P(B2 | B1)” is the General Multiplication Rule as it applies to this question.
With a probability tree diagram, you multiply the probabilities as you travel down the “branches” of the tree. As an additional example, the probability that both balls are white is P(W1 and W2) = P(W1) x P(W2 | W1) = (3/5) x (2/4) = 6/20 = 3/10 = 0.3 = 30%.
General Multiplication Rule
For any two events A and B: P(A and B) = P(A) x P(B | A).
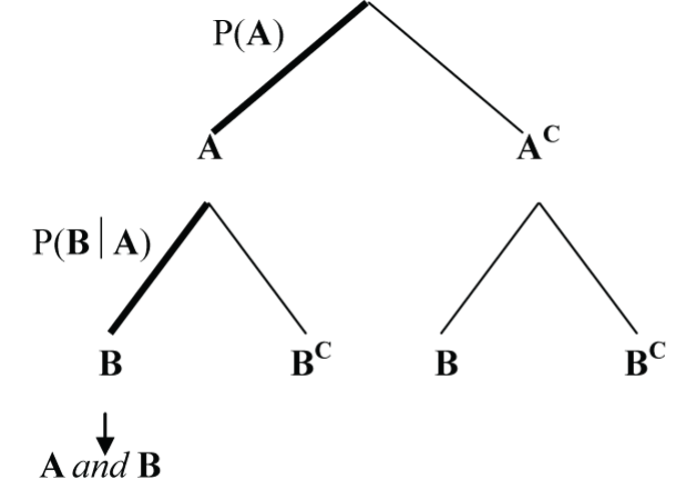
Independence
Two events A and B are independent if P(B | A) = P(B).
Example
Consider an experiment with 12 male and 13 female patients. If two subjects are randomly selected from the 25 (without replacement), find the probability that:
- Both are male.
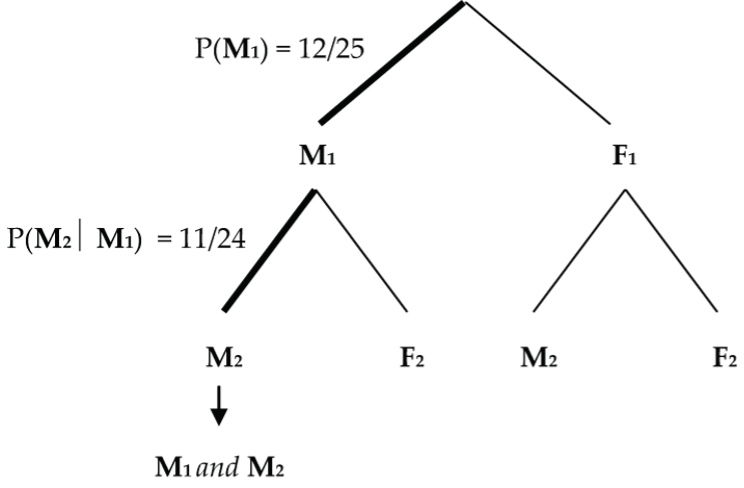
Figure 4: Probability tree determines the likelihood that two randomly-selected participants are male P(M1 and M2) = P(M1) x P(M2 | M1) = (12/25) x (11/24) = 132/600 = 22/100 = 0.22 = 22%.
- At least one of the two is female.
P(at least one female) = 1 – P(no females) = 1 – P(M1 and M2) = 1 – 0.22 = 0.78 = 78%.
Example: General Multiplication Rule
Consider an experiment with three treatment levels (physio, drug, and sham/control), in which 8 patients received physio, 11 patients received drug, and 6 patients received sham/control. If two subjects are randomly selected from the 25 patients (without replacement), find the probability that they both receive the same treatment.
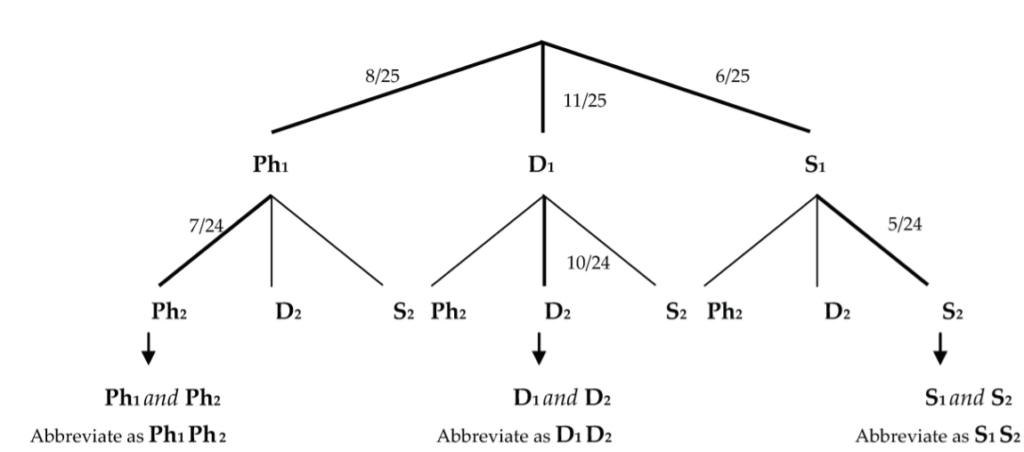
P((Ph1 and Ph2) or (D1 and D2) or (S1 and S2)) = (P(Ph1) x P(Ph2 | Ph1)) + (P(D1) x P(D2 | D1)) + (P(S1) x P(S2 | S1)) = ((8/25) x (7/24)) + ((11/25) x (10/24)) + ((6/25) x (5/24)) = 196/600 = 0.3267 = 32.67%.
We use the General Multiplication Rule to calculate P(Ph1 and Ph2), P(D1 and D2), and P(S1 and S2).
The outcomes (Ph1 and Ph2), (D1 and D2), and (S1 and S2) are disjoint since they can’t happen simultaneously. So, we use the Addition Rule for Disjoint Events from Lesson 2.1: Probabilities of Events to add their probabilities.
So, there is a 32.67% chance that both subjects will receive the same treatment.
Additional Examples
Example 1
In 2 spins of the pointer below (Fig. 6), find the probability that the $5 outcome comes-up only once.
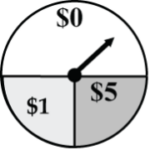
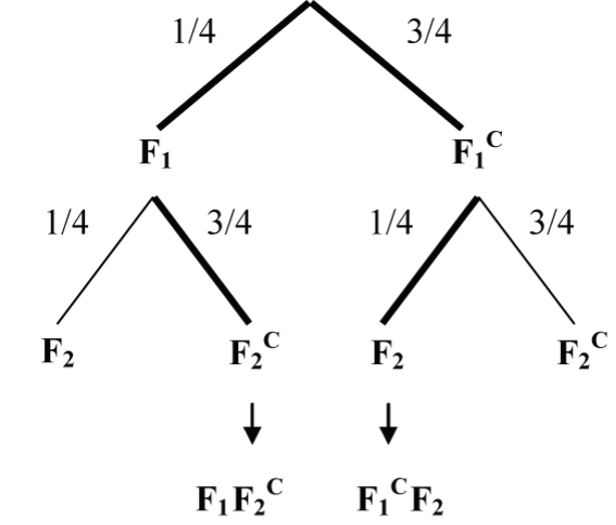
P((F1 and F2C) or (F1C and F2)) = (P(F1) x P(F2C)) + (P(F1C) x P(F2)) = ((1/4) x (3/4)) + ((3/4) x (1/4)) = 6/16 = 0.375 = 37.5%.
So, there is a 37.5% chance that the $5 comes up only once.
Example 2
Consider the sample space S below (Fig. 8):
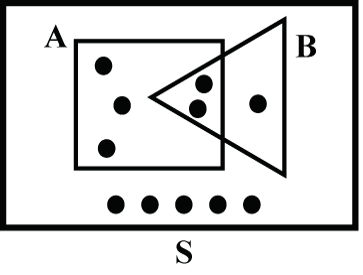
If each of the 11 outcomes in the sample space S are equally likely, then we can count the dots to get: P(A) = 5/11, P(B) = 3/11, P(A and B) = 2/11, and P(A or B) = 6/11.
P(B | A) = 2/5.
Are events A and B independent?
No, since P(B | A) = 2/5 ![]() P(B) = 3/11.
P(B) = 3/11.
Can we use the General Multiplication Rule to calculate P(A and B)?
Of course (although it is much easier in this case to just count the dots as above): P(A and B) = P(A) x P(B | A) = (5/11) x ( 2/5) = 2/11.
Other conditional probabilities: P(A | B) = 2/3, P(A | BC) = 3/8, P(B | AC) = 1/6. Make sure you can derive each of these from the sample space S above.
Example: Independence
Consider 200 students’ movie preferences in the following contingency table (Table 1).
| Movie Preferences | ||||
| Drama | Action | Comedy | ||
| Male | 20 | a | b | 120 |
| Female | 40 | c | d | 80 |
| 60 | 100 | 40 | 200 | |
- For these 200 students, are the events “student is male” and “student prefers drama” independent?
- M = Student is male
- D = Student prefers drama
For M and D to be independent, we must have P(M | D) = P(M).Here P(M | D) = 20/60 = 1/3, and P(M) = 120/200 = 3/5.
Since P(M | D) P(M), we conclude that M and D are not independent––they are dependent.
P(M), we conclude that M and D are not independent––they are dependent.This question could also have been answered by seeing if P(D | M) = P(D).
Here P(D | M) = 20/120 = 1/6, and P(D) = 60/200 = 3/10.
Since P(D | M) P(D), we conclude that M and D are not independent––they are dependent.
P(D), we conclude that M and D are not independent––they are dependent. - Fill-in the missing entries in Table 1 in such a way that the two events M = “Student is male” and C = “Student prefers comedy” are independent. For M and C to be independent, we must have P(M | C) = P(M). So b/40 = 120/200, b = (120/200) x 40 = 24. By subtraction, we get d = 16, a = 76, c = 24.
Let’s step back and interpret these results in context.
Part 1 of this example is saying that only 1/3 of those people preferring drama are males, yet males make up 3/5 = 60% of this entire group, so there is an association between “drama preference” and “male.” They are dependent.
Part 2 is saying that 24/40 = 3/5 = 60% of those people preferring comedy are males, which is exactly equal to the percentage of males in the entire group, so there is no association between “comedy preference” and “male.” They are independent.
Conditional Probability Revisited
So far, the calculation of a conditional probability like P(A | B) or P(B | A) has come naturally by direct count or evaluation. Most of the time this will be the case, but there are some applications where a conditional probability can’t be calculated this way and we need a formula to calculate it. Which formula? It’s just the General Multiplication Rule rearranged.
General Multiplication Rule: P(A and B) = P(A) x P(B | A) = P(B | A) x P(A).
Note that by considering events A and B in the opposite order, the General Multiplication Rule can also be expressed as P(A and B) = P(B and A) = P(B) x P(A | B) = P(A | B) x P(B).
Therefore, we can write P(A | B) x P(B) = P(B | A) x P(A).
And so P(A | B) = P(B | A) x P(A) / P(B).
Next, write P(B) = P((A and B) or (AC and B)) = P(A and B) + P(AC and B) = (P(B | A) x P(A)) + (P(B | AC) x P(AC)).
Then, P(A | B) = P(B | A) x P(A) / ((P(B | A) x P(A)) + (P(B | AC) x P(AC))).
This is known as Bayes Theorem.
Example: Reversing the Conditioning
Only 1 in 1,000 adults is afflicted with a rare disease for which a diagnostic test has been developed. The test is such that, when a person actually has the disease, a positive test result will occur 99% of the time, while a person without the disease will show a positive test result only 2% of the time (a so-called “false positive”). If a randomly selected person is tested and the result is positive, what is the probability that the person has the disease?
Lots of words! Let’s start by identifying the given information symbolically:
- D = Person has disease
- Pos = Person tests positive
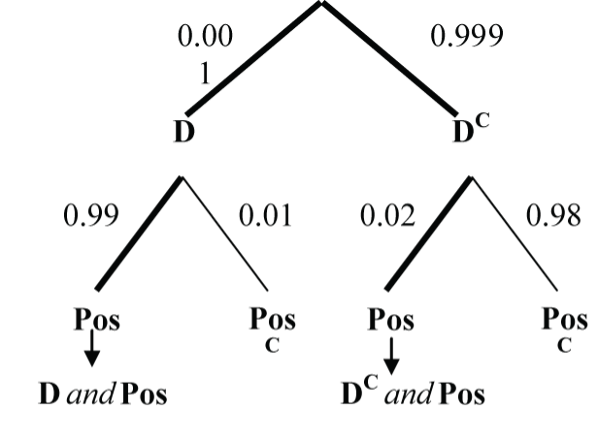
Find P(D | Pos) given:
- P(D) = 1/1000 = 0.001
- P(Pos | D) = 0.99
- P(Pos | DC) = 0.02
Since P(D | Pos) doesn’t come “naturally,” we use Bayes Theorem to calculate it.
- P(D | Pos) = P(Pos | D) x P(D) / ((P(Pos | D) x P(D)) + (P(Pos | DC) x P(DC)))
- P(D | Pos) = (0.99 x 0.001) / ((0.99 x 0.001) + (0.02 x 0.999))
- P(D | Pos) = 0.0472
So, the probability that the person has the disease is only about 4.72%. Surprised that it is so low? It is low because the disease is rare, and the false positive rate is relatively high at 2%.

