Lesson 3.3: Hypothesis Testing

Lesson Learning Objectives
- Understand the basic concepts underlying statistical hypothesis testing.
- Understand the distinction between the roles of the null hypothesis and the alternative hypothesis.
- Work through the four-step process—prepare, check, calculate, conclude—for the one-proportion Z-test.
- Interpret a p-value.
- Understand how to choose hypotheses.
- Understand the relationship between a p-value and the significance level.
- Understand the distinction between statistical significance and practical significance.
- Understand the interconnections between Type 1 and 2 errors, significance levels, power, and sample size.
- Understand the relationship between a two-sided hypothesis test and a confidence interval for a proportion.
Lesson 3.3 Checklist
| Learning activity | Graded? | Estimated time |
|---|---|---|
| Read OpenIntro Statistics section 5.3 and supplementary notes | No | 30 mins |
| Watch instructional video | No | 15 mins |
| Answer two lesson check-in questions | Yes | 15 mins |
| Work through virtual statistical software lab | No | 45 mins |
| Answer two virtual statistical software lab questions | Yes | 15 mins |
| Work on practice exercises | No | 1.5 hours |
| Explore suggested websites | No | 15 mins |
| Complete and submit Unit 3 Assignment | Yes | 2 hours |
Learning Activities
Readings 📖 and Instructional Video 🎦
Hypothesis Test for a Proportion
Read Section 5.3: Hypothesis Testing for a Proportion in OpenIntro Statistics (Diez et al., 2019) CC BY-SA 3.0. In the last lesson, we learned how to calculate a plausible range of values for the population proportion using a confidence interval. Now, we’ll learn how to use a hypothesis testing framework to formally evaluate two competing claims about the population proportion. This section will really test your critical thinking skills, and you may need to re-read this material a few times before you fully understand it. Section 5.3.7 on one-sided hypothesis tests is considered a special topic in the textbook and for the remainder of the book only two-sided tests are used. However, you’ll get to see some examples of one-sided tests in Supplementary Notes 3.3.
As you read, look up new terminology in the Glossary and self-assess your understanding by attempting the guided practice exercises.
Watch the video, Hypothesis Test for Proportions (Mays, 2012), on this topic (duration 00:15:00).
Hypothesis Test for a Proportion
Read Supplementary Notes 3.3, which builds intuition into hypothesis testing using the analogy of a courtroom trial in which the null hypothesis represents “innocence” and the alternative hypothesis represents “guilt beyond a reasonable doubt.”
Significance Levels: Why 0.05?
Try this online exercise, Why Do We so Often Use 0.05 for Hypothesis Testing? [Application] (Diez et al., 2019) CC BY-SA 3.0, to gain an improved understanding of significance levels in hypothesis testing.
Lesson Check-in Questions ✍
Virtual Statistical Software Lab 💻
Work through the virtual statistical software lab: Software Lab 3.3: Hypothesis Testing. In this lab you’ll work through the steps of a hypothesis test and gain a deeper understanding of hypothesis test errors, the significance level, and power. As you work through the lab, answer the exercises in the shaded boxes. These exercises are not graded but the solutions are available: Software Lab 3.3 Solutions. The lab should take you no more than 45 minutes to complete.
Virtual Statistical Software Lab Questions ✍
Practice Exercises 🖊
Work on the following exercises in OpenIntro Statistics: Exercises 5.15, 5.17, 5.19, 5.21, 5.23, and 5.25, and Chapter Exercises 5.29, 5.31, 5.35, and 5.37 (Diez et al., 2019) CC BY-SA 3.0. Check your answers using these solutions (Diez et al., 2019) CC BY-SA 3.0. You’ll deepen your understanding much more effectively if you genuinely attempt the questions by yourself before checking the solutions.
Work on the WeBWorK exercises, which are linked from your Moodle course. Check your answers using the solutions provided.
Suggested Websites 🌎
- To better understand hypothesis test errors and their relationship to the significance level and power of a test, check-out this interactive Errors and Power [Application] (CPM Educational Program, 2023) simulator. For example, consider Supplementary Notes 3.3 Example 3 about drug detection. Set the null hypothesis to
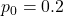 , the alternative hypothesis to
, the alternative hypothesis to  , the sample size to
, the sample size to 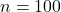 , the significance level to
, the significance level to 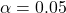 , and the “suspected true population proportion” to
, and the “suspected true population proportion” to 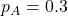 . You should see that P(type 1 error) = 0.05, P(type 2 error) = 0.2277, and power = 0.7723. We can reduce P(type 1 error) and P(type 2 error) (and increase power) if we increase the sample size to
. You should see that P(type 1 error) = 0.05, P(type 2 error) = 0.2277, and power = 0.7723. We can reduce P(type 1 error) and P(type 2 error) (and increase power) if we increase the sample size to 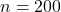 and reduce the significance level to
and reduce the significance level to 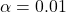 . Try it to see and confirm that P(type 1 error) = 0.01, P(type 2 error) = 0.1456, and power = 0.8544.
. Try it to see and confirm that P(type 1 error) = 0.01, P(type 2 error) = 0.1456, and power = 0.8544. - To practice doing a hypothesis test for a proportion, use this Single Proportion Hypothesis Test Calculator [Application] (Infrrr, 2023). For example, consider the examples in Supplementary Notes 3.3:
- For Example 1 on purchasing parkland, set the null proportion to
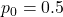 , the sample proportion to
, the sample proportion to 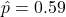 , the sample size to
, the sample size to 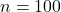 , the alternative hypothesis to
, the alternative hypothesis to  , and the significance level to
, and the significance level to 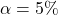 . The test statistic
. The test statistic 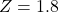 is labeled “sample proportion z-score” and the p-value = 0.0359 is labeled “sample proportion probability.”
is labeled “sample proportion z-score” and the p-value = 0.0359 is labeled “sample proportion probability.” - For Example 2 on the Green Party, set the null proportion to
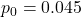 , the sample proportion to
, the sample proportion to 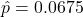 , the sample size to
, the sample size to 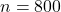 , the alternative hypothesis to
, the alternative hypothesis to 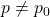 , and the significance level to
, and the significance level to 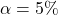 . Confirm the test statistic is
. Confirm the test statistic is 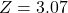 and the p-value is 0.0021.
and the p-value is 0.0021. - For Example 3 on drug detection, set the null proportion to
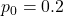 , the sample proportion to
, the sample proportion to 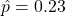 , the sample size to
, the sample size to 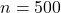 , the alternative hypothesis to
, the alternative hypothesis to  , and the significance level to
, and the significance level to 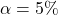 . Confirm the test statistic is
. Confirm the test statistic is 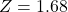 and the p-value is 0.0468.
and the p-value is 0.0468.
- For Example 1 on purchasing parkland, set the null proportion to
Unit Assignment ✍
Media Attributions
References
CPM Educational Program. (2023). Errors and power [Application]. https://stats.cpm.org/power/
Diez, D. M., Çetinkaya-Rundel, M., Barr, C. D. (2019). OpenIntro Statistics (4th ed.). OpenIntro. https://www.openintro.org/book/os/
Infrrr. (2023). Single proportion hypothesis test calculator [Application]. https://www.infrrr.com/proportions/single-proportion-hypothesis-test-calculator
Mays, S. (2012, Jan. 11). Hypothesis test for proportions [Video]. YouTube. https://www.youtube.com/watch?v=t09Vyd7H52A
Treble, M. (2011). Blind justice 3 [Photograph]. Flickr. https://flic.kr/p/9jU8xd

