Lesson 4.1: Inference for Proportions

Lesson Learning Objectives
- Review confidence intervals and hypothesis testing for a single proportion.
- Determine the sample size needed to achieve a desired accuracy and confidence in estimating a population proportion.
- Describe the sampling distribution for the difference between two independent sample proportions.
- Construct a confidence interval for the difference between two population proportions.
- Test the hypothesis that two population proportions are equal.
- Know the conditions underlying the confidence interval and hypothesis test for two proportions.
Lesson 4.1 Checklist
| Learning activity | Graded? | Estimated time |
|---|---|---|
| Read OpenIntro Statistics sections 6.1 and 6.2 and supplementary notes | No | 30 mins |
| Watch instructional video | No | 20 mins |
| Answer two lesson check-in questions | Yes | 15 mins |
| Work through virtual statistical software lab | No | 45 mins |
| Answer two virtual statistical software lab questions | Yes | 15 mins |
| Work on practice exercises | No | 1.5 hours |
| Explore suggested websites | No | 15 mins |
Learning Activities
Readings 📖 and Instructional Video 🎦
Inference for Proportions
Read Section 6.1: Inference for a Single Proportion in OpenIntro Statistics (Diez et al., 2019) CC BY-SA 3.0. This section reviews the material on confidence intervals and hypothesis testing for a single proportion from Lesson 3.2: Confidence Intervals and Lesson 3.3: Hypothesis Testing.
Then read Section 6.2: Difference of Two Proportions. Here you’ll learn how to use similar ideas from the one-proportion setting to analyze the difference of two proportions based on two independent samples. Don’t worry about reading Sections 6.2.4 and 6.2.5, since these cover special topics beyond the scope of this course. As you read, look-up new terminology in the Glossary and self-assess your understanding by attempting the guided practice exercises.
Watch the following video, Sampling Distribution for Proportions (Çetinkaya-Rundel, 2013), on this topic (duration 00:16:15).
Inference for Proportions
Read Supplementary Notes 4.1, which reviews confidence intervals and hypothesis testing for one proportion and the difference of two proportions.
Lesson Check-in Questions ✍
Virtual Statistical Software Lab 💻
Work through the virtual statistical software lab: Software Lab 4.1. In this lab you’ll have a chance to practice calculating a confidence interval and doing a hypothesis test in both the one proportion and two proportion settings. As you work through the lab, answer the exercises in the shaded boxes. These exercises are not graded, but the solutions are available: Software Lab 4.1 Solutions. The lab should take you no more than 45 minutes to complete.
Virtual Statistical Software Lab Questions ✍
Practice Exercises 🖊
Work on the following exercises in OpenIntro Statistics: Exercises 6.1, 6.3, 6.5, 6.7, 6.9, 6.11, 6.13, 6.15, 6.17, 6.19, 6.21, 6.23, 6.25, 6.27, and 6.29, and Chapter Exercises 6.39, 6.43, 6.45, and 6.49 (Diez et al., 2019) CC BY-SA 3.0. Check your answers using these solutions (Diez et al., 2019) CC BY-SA 3.0. You’ll deepen your understanding much more effectively if you genuinely attempt the questions by yourself before checking the solutions.
Work on the WeBWorK exercises, which are linked from your Moodle course. Check your answers using the solutions provided.
Suggested Websites 🌎
- Practice choosing a sample size when estimating a proportion with Sample Size Calculator for Estimating a Single Proportion [Application] (Dhand & Khatkar, 2023), and work through the following:
- Consider the football stadium example in Section 6.1.5 in the textbook. Set the level of confidence to 0.95, the expected proportion to 0.5, the precision or margin of error to “absolute value” and 0.04, and click “Calculate.” Confirm that the sample size required for this scenario is 601.
- Consider the payday lender regulation example in Section 6.1.5 in the textbook. Set the level of confidence to 0.95, the expected proportion to 0.7, the precision or margin of error to “absolute value” and 0.05, and click “Calculate.” Confirm that the sample size required for this scenario is 323.
- Consider the public place smoking ban example in Supplementary Notes 4.1. Set the level of confidence to 0.95, the expected proportion to 0.5, the precision or margin of error to “absolute value” and 0.04, and click “Calculate.” Confirm that the sample size required for this scenario is 601. Then change the expected proportion to 0.75 and confirm that the sample size decreases to 451.
- Practice doing a hypothesis test for the difference of two proportions with Hypothesis Test and Confidence Interval Calculator- Difference Between Population Proportions [Application] (Green, 2021), and work through the following:
- Consider the example on mammograms in Section 6.2.3 in the textbook. Set the first sample size to 44,925 with 500 successes (“successes” stands for deaths in this case) and the second sample size to 44,910 with 505 successes. Then select “≠” and 0.95 for “CL” (confidence level) and click “Calculate.” You’ll see the test statistic listed under “z” (–0.1639) and the p-value listed under “p” (0.8698). (These values are more accurate than those in the book, which use rounded numbers for intermediate calculations. Rounding numbers for intermediate calculations is not generally recommended since it can lead to inaccurate answers.)
- Consider the example on smoking cessation in Supplementary Notes 4.1. Set the first sample size to 150 with 90 successes and the second sample size to 100 with 50 successes. Then select “≠” and 0.95 for “CL” (confidence level) and click “Calculate.” You’ll see the test statistic listed under “z” (1.5605) and the p-value listed under “p” (0.1186).
- This calculator also displays a confidence interval going from “LB” (lower bound) to “UB” (upper bound). However, this uses the pooled proportion (
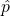 ) in the calculation of the confidence interval. This differs from the method in the textbook and supplementary notes, which uses the individual group proportions (
) in the calculation of the confidence interval. This differs from the method in the textbook and supplementary notes, which uses the individual group proportions (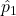 and
and 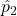 ).
).
Media Attributions
Golden Ratio, by sinkdd (2011), on Flickr, CC BY-NC-ND 2.0
References
Çetinkaya-Rundel, M. (2013, Jan. 9). Sampling distribution for proportions [Video]. YouTube. https://www.youtube.com/watch?v=_iFAZgpWsx0
Dhand, N., & Khatkar, M. (2023). Sample size calculator for estimating a single proportion [Application]. Statulator. https://statulator.com/SampleSize/ss1P.html
Diez, D. M., Çetinkaya-Rundel, M., Barr, C. D. (2019). OpenIntro Statistics (4th ed.). OpenIntro. https://www.openintro.org/book/os/
Green, L. (2021, Dec. 9). 33: Hypothesis test and confidence interval calculator- difference between population proportions [Application]. LibreTexts Statistics. https://stats.libretexts.org/Learning_Objects/02%3A_Interactive_Statistics/33%3A__Hypothesis_Test_and_Confidence_Interval_Calculator-_Difference_Between_Population_Proportions
sinkdd. (2011). Golden ratio [Photograph]. Flickr. https://flic.kr/p/ah3oJM

