Lesson 5.1: Inference for One Mean or a Mean Difference from Two Paired Groups

Iain Pardoe

Lesson 5.1: Inference for One Mean or a Mean Difference from Two Paired Groups

*“Inside an Ammonite: Paired” by cobalt123 is licensed under CC BY-NC-SA 2.0*

Lesson Learning Objectives

Understand the concept of a sampling distribution for a sample mean.
Know and apply the central limit theorem (CLT) for a sample mean.
Check the conditions needed for t-based confidence intervals and hypotheses tests for a mean.
Construct and interpret a confidence interval for a mean.
Perform a one-sample t-test for a mean.
Determine the sample size needed to estimate a mean with a desired margin of error and confidence.
Distinguish between independent vs. paired samples designs.
Check the conditions needed for t-based confidence intervals and hypotheses tests for paired samples.
Construct and interpret a paired t-confidence interval for the mean difference.
Perform a paired t-test for the mean difference.

Lesson 5.1 Checklist

Learning activity	Graded?	Estimated time
Read OpenIntro Statistics sections 7.1 and 7.2 and supplementary notes	No	30 mins
Watch instructional videos	No	30 mins
Answer two section check-in questions	Yes	15 mins
Work through virtual statistical software lab	No	45 mins
Answer two virtual statistical software lab questions	Yes	15 mins
Work on practice exercises	No	1.5 hours
Explore suggested websites	No	15 mins

Learning Activities

Readings 📖 and Instructional Video 🎦

Inference for a Mean

Read Section 7.1: One-Sample Means with the T-Distribution in OpenIntro Statistics (Diez et al., 2019) CC BY-SA 3.0. Recall that inference for a proportion uses the normal distribution. This lesson covers inference for a mean using a different symmetric bell-shaped distribution called a t-distribution.

Watch the following video, 5 1 A T-Distribution (Çetinkaya-Rundel, 2018-a), which explains the t-distribution (duration 00:07:20).

Lesson 4.1 covered confidence intervals and hypothesis tests for a population proportion based on sample data for a categorical variable with two levels. This lesson considers confidence intervals and hypothesis tests for a population mean based on sample data for a numerical variable. As you read, look-up new terminology in the Glossary and self-assess your understanding by attempting the guided practice exercises.

Watch the following video, 5 1 B Inference for a Mean (Çetinkaya-Rundel, 2018-b), on this topic (duration 00:09:44).

Then read Section 7.2: Paired Data (Diez et al., 2019) CC BY-SA 3.0. If there are two groups in our data set, and each observation in one dataset is uniquely paired with exactly one observation in the other dataset, then the data is said to be paired.

Suppose we want to make an inference about the difference between the mean of a numerical variable in one group and the mean of that variable in the other group. Then we can apply what we just learned about inference for a mean to the difference between the numerical variable in one group and the numerical variable in the other group.

As you read, look up new terminology in the Glossary and self-assess your understanding by attempting the guided practice exercises.

Watch the following video, 5 2 Inference for Paired Data (Çetinkaya-Rundel, 2018-c), on this topic (duration 00:09:02).

Inference for Means

Read Supplementary Notes 5.1, which reviews confidence intervals and hypothesis testing for a mean. Note: The textbook uses the notation $\overline{x}$ to denote the sample mean, but in Supplementary Notes 5.1 we use the notation $\overline{y}$ . Don’t worry about this difference, as we’re only concerned with a single numerical variable and it really doesn’t matter what letter we use.

Lesson Check-in Questions ✍

Answer the two check-in questions for Lesson 5.1 in your Moodle course. The questions are based on the material covered in the readings and instructional videos. The questions are multiple-choice, fill-in-the-blank, matching, or calculation questions, and they are auto-graded in Moodle. Once you access the questions, you have 15 minutes to submit your answers. Overall the Lesson Check-in Questions count 6% toward your total grade.

Virtual Statistical Software Lab 💻

Work through the virtual statistical software lab: Software Lab 5.1. In this lab you’ll have a chance to practice calculating a confidence interval and doing a hypothesis test in both the one mean and paired data mean difference settings. As you work through the lab, answer the exercises in the shaded boxes. These exercises are not graded but the solutions are available: Software Lab 5.1 Solutions. The lab should take you no more than 45 minutes to complete.

Virtual Statistical Software Lab Questions ✍

Answer the two virtual statistical software lab questions for Software Lab 5.1 in your Moodle course. The questions are based on the lab you just completed. The questions are multiple-choice, fill-in-the-blank, matching, or calculation questions, and they are auto-graded in Moodle. Once you access the questions, you have 15 minutes to submit your answers. Overall the Software Lab Questions count 6% toward your total grade.

Practice Exercises 🖊

Work on the following exercises in OpenIntro Statistics: Exercises 7.1, 7.3, 7.5, 7.7, 7.9, 7.11, 7.13, 7.15, 7.17, 7.19, and 7.21 and Chapter Exercises 7.49, 7.51, 7.55, and 7.57 (Diez et al., 2019) CC BY-SA 3.0. When answering these questions, recall from Section 5.3.7 that the textbook only uses two-sided hypothesis tests, not one-sided ones. Check your answers using these solutions (Diez et al., 2019) CC BY-SA 3.0. You’ll deepen your understanding much more effectively if you genuinely attempt the questions by yourself before checking the solutions.

Work on the WeBWorK exercises, which are linked from your Moodle course. Check your answers using the solutions provided.

Suggested Websites 🌎

Check-out Central Limit Theorem for Means [Application] (Çetinkaya-Rundel, 2019) to appreciate how the central limit theorem (CLT) works. To get started, select “Uniform” for the “Parent distribution (population),” set the “Lower and Upper Bounds” to 0–3, set the “Sample size” to 200, and the “Number of samples” to 100 (you may need to use the arrows on your keyboard to fine-tune these numbers). You should see a uniform histogram for the “Population Distribution” with a mean of 1.5 and a standard deviation around 0.86 or 0.87. Click the “Samples” tab to see dot plots of the first 8 samples. Then click the “Sampling Distribution” tab to see a roughly normal histogram for the sampling distribution of the mean with a mean of 1.5 and a standard error around 0.06.
To practice calculating a confidence interval for a mean, use Confidence Interval Calculator [Application] (Statistics Kingdom, n.d.-a).
- Consider the example on Risso’s dolphins in Section 7.1.4 in the textbook. Set the average to 4.4, the sample size to 19, and the standard deviation to 2.3. Then click “Calculate” to see the results and the calculation steps. The results are more accurate than those in the textbook, which use rounded numbers for intermediate calculations. Rounding numbers for intermediate calculations is not generally recommended, since it can lead to inaccurate answers.
- Consider the example on textbook prices in Section 7.2 in the textbook. Set the average to 3.58, the sample size to 68, and the standard deviation to 13.42. Then click “Calculate” to see the results and the calculation steps.
To practice doing a hypothesis test for a mean, use One Sample T Test Calculator [Application] (Statistics Kingdom, n.d.-b).
- Consider the Cherry Blossom Race example in Section 7.1.5 in the textbook. Set the expected mean ( 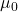$\mu_0$ ) to 93.29, the sample average to 97.32, the sample size to 100, and the sample standard deviation to 16.98. Then click “Calculate” to see the results and the calculation steps. Again, the results here are more accurate than those in the textbook.
- Consider the example on textbook prices in Section 7.2 in the textbook. Set the expected mean ( 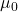$\mu_0$ ) to 0, the sample average to 3.58, the sample size to 68, and the sample standard deviation to 13.42. Then click “Calculate” to see the results and the calculation steps.

Media Attributions

Inside an Ammonite: Paired, by cobalt123 (2007), on Flickr, CC BY-NC-SA 2.0

References

Çetinkaya-Rundel, M. (2018-a, Feb. 19). 5 1A t distribution [Video]. YouTube. https://www.youtube.com/watch?v=uVEj2uBJfq0

Çetinkaya-Rundel, M. (2018-b, Feb. 19). 5 1B Inference for a mean [Video]. YouTube. https://www.youtube.com/watch?v=RYVIGj1l4xs

Çetinkaya-Rundel, M. (2018-c, Feb. 19). 5 2 Inference for paired data [Video]. YouTube. https://www.youtube.com/watch?v=K0QZ9_4w0HU

Çetinkaya-Rundel, M. (2019, Jun. 25). Central limit theorem for means [Application]. OpenIntro. https://gallery.shinyapps.io/CLT_mean/

cobalt123. (2007). Inside an ammonite: Paired [Photograph]. Flickr. https://flic.kr/p/22Uty7

Diez, D. M., Çetinkaya-Rundel, M., Barr, C. D. (2019). OpenIntro Statistics (4^th ed.). OpenIntro. https://www.openintro.org/book/os/

Statistics Kingdom. (n.d.-a). Confidence interval calculator [Application]. https://www.statskingdom.com/confidence-interval-calculator.html

Statistics Kingdom. (n.d.-b). One sample T test calculator [Application]. https://www.statskingdom.com/130MeanT1.html

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Introduction to Probability and Statistics Copyright © 2023 by Thompson Rivers University is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.