Lesson 5.2: Inference for Difference in Means from Two Independent Groups

Lesson Learning Objectives
- Describe the sampling distribution for the difference between two independent sample means.
- Construct a confidence interval for the difference between population means for two independent groups.
- Test a hypothesis for the difference in the population means for two independent groups.
- Check the conditions underlying the confidence interval and hypothesis test for two independent means.
Lesson 5.2 Checklist
| Learning activity | Graded? | Estimated time |
|---|---|---|
| Read OpenIntro Statistics sections 7.3 and supplementary notes | No | 30 mins |
| Watch instructional video | No | 10 mins |
| Answer two section check-in questions | Yes | 15 mins |
| Work through virtual statistical software lab | No | 45 mins |
| Answer two virtual statistical software lab questions | Yes | 15 mins |
| Work on practice exercises | No | 1.5 hours |
| Explore suggested websites | No | 15 mins |
Learning Activities
Readings 📖 and Instructional Video 🎦
Difference of Means from Two Independent Groups
Read Section 7.3: Difference of Two Means in OpenIntro Statistics (Diez et al., 2019) CC BY-SA 3.0. In Lesson 5.1, we considered inference for a difference in means based on paired data. In this lesson, we will consider inference for a difference in means based on data from two independent groups. The confidence interval and hypothesis test described here are sometimes referred to as Welch’s two-sample t-interval and t-test.
Note: The sample standard deviations in the North Carolina births example in Section 7.3.2 are reversed: It should be ![]() for smokers and
for smokers and ![]() for nonsmokers. The estimated standard error should be
for nonsmokers. The estimated standard error should be ![]() and the test statistic should be
and the test statistic should be ![]() .
.
Read Section 7.3.4: Pooled Standard Deviation Estimate (Special Topic), but don’t worry too much about the details. This is for when background research indicates the population standard deviations are nearly equal. The standard error and degrees of freedom calculations change, but the overall approach is essentially the same. In practice, both approaches give broadly similar results as long as the sample sizes are reasonably large. Don’t worry about reading Section 7.4: Power Calculations for a Difference of Means.
As you read, look up new terminology in the Glossary and self-assess your understanding by attempting the guided practice exercises.
Watch the following video, 5 3 Difference of Two Independent Means (Çetinkaya-Rundel, 2018), on this topic (duration 00:08:56).
Comparing Means in Two Independent Groups
Read Supplementary Notes 5.2, which runs through a few examples of confidence intervals and hypothesis testing for the difference between means in two independent groups.
Lesson Check-in Questions ✍
Virtual Statistical Software Lab 💻
Work through the virtual statistical software lab: Software Lab 5.2. In this lab you’ll work though two-sample t-tests and t-intervals for two examples. As you work through the lab, answer the exercises in the shaded boxes. These exercises are not graded but the solutions are available: Software Lab 5.2 Solutions. The lab should take you no more than 45 minutes to complete.
Virtual Statistical Software Lab Questions ✍
Practice Exercises 🖊
Work on the following exercises in OpenIntro Statistics: Exercises 7.23, 7.25, 7.27, 7.29, and 7.31 and Chapter Exercise 7.47 (Diez et al., 2019) CC BY-SA 3.0. Check your answers using these solutions (Diez et al., 2019) CC BY-SA 3.0. You’ll deepen your understanding much more effectively if you genuinely attempt the questions by yourself before checking the solutions.
Work on the WeBWorK exercises, which are linked from your Moodle course. Check your answers using the solutions provided.
Suggested Websites 🌎
- Practice calculating a confidence interval for a difference of means from two independent groups using Two Sample T-Test Calculator (Welch’s T-Test) [Application] (Statistics Kingdom, n.d.).
- Consider the sheep heart attacks example in Section 7.3.1 in the textbook. Type the group names (“ESCs” and “control”), set the sample averages to 3.50 and –4.33, the sample sizes to 9 and 9, and the sample standard deviations to 5.17 and 2.76. Then click “Calculate” to see the results needed to calculate the interval. The centre of the interval is given by the difference in the sample means, 7.83. The standard error is given by the “standard deviation of the difference,” 1.954. The critical value of t is given by the upper bound of the “95% region of acceptance for T,” 2.1745. Put these together to calculate the 95% confidence interval:
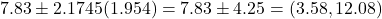 . The results are more accurate than those in the textbook, which uses the wrong degrees of freedom.
. The results are more accurate than those in the textbook, which uses the wrong degrees of freedom. - Consider the weight-loss pills example in Supplementary Notes 5.2. Type the group names (“placebo” and “CLA”), set the sample averages to 2.7 and 2.1, the sample sizes to 43 and 40, and the sample standard deviations to 4.9 and 5.0. Then click “Calculate” to see the results needed to calculate the interval. The centre of the interval is given by the difference in the sample means, 0.6. The standard error is given by the “standard deviation of the difference,” 1.088. The critical value of t is given by the upper bound of the “95% region of acceptance for T,” 1.9899. Put these together to calculate the 95% confidence interval:
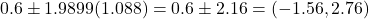 .
.
- Consider the sheep heart attacks example in Section 7.3.1 in the textbook. Type the group names (“ESCs” and “control”), set the sample averages to 3.50 and –4.33, the sample sizes to 9 and 9, and the sample standard deviations to 5.17 and 2.76. Then click “Calculate” to see the results needed to calculate the interval. The centre of the interval is given by the difference in the sample means, 7.83. The standard error is given by the “standard deviation of the difference,” 1.954. The critical value of t is given by the upper bound of the “95% region of acceptance for T,” 2.1745. Put these together to calculate the 95% confidence interval:
- Practice doing a hypothesis test for a difference of means from two independent groups using Two Sample T-Test Calculator (Welch’s T-Test) [Application] (Statistics Kingdom, n.d.).
- Consider the smoking mothers example in Section 7.3.2 in the textbook. Type the group names (“nonsmoker” and “smoker”), set the sample averages to 7.18 and 6.78, the sample sizes to 100 and 50, and the sample standard deviations to 1.43 and 1.60. Then click “Calculate” to see the results (test statistic = 1.4944, df = 88.9353, p-value = 0.1386) and the calculation steps. Again, the results from this application are more accurate than those in the textbook.
- Consider the exam versions example in Section 7.3.3 in the textbook. Type the group names (“A” and “B”), set the sample averages to 79.4 and 74.1, the sample sizes to 30 and 27, and the sample standard deviations to 14 and 20. Then click “Calculate” to see the results (test statistic = 1.1471, df = 45.9726, p-value = 0.2573) and the calculation steps.
- Consider the fish oil example in Supplementary Notes 5.2. Type the group names (“fish oil” and “placebo”), set the sample averages to 114 and 108, the sample sizes to 33 and 39, and the sample standard deviations to 10.2 and 11.3. Then click “Calculate” to see the results (test statistic = 2.3668, df = 69.6865, p-value = 0.02073) and the calculation steps.
Media Attributions
Group of People Divided Into Two Teams, by RODNAE Productions (2021), on Pexels, is free to use via Pexels license.
References
Çetinkaya-Rundel, M. (2018, Feb. 19). 5 3 Difference of two independent means [Video]. YouTube. https://www.youtube.com/watch?v=emZ24asR2F4
Diez, D. M., Çetinkaya-Rundel, M., Barr, C. D. (2019). OpenIntro Statistics (4th ed.). OpenIntro. https://www.openintro.org/book/os/
RODNAE Productions. (n.d.). Group of people divided into two teams [Photograph]. Pexels. https://www.pexels.com/photo/group-of-people-divided-into-two-teams-7551186/
Statistics Kingdom. (n.d.). Two sample T-test calculator (Welch’s T-test) [Application]. https://www.statskingdom.com/150MeanT2uneq.html

